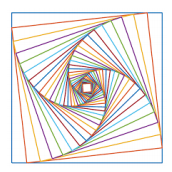
Draw nested squares to create pursuit curves. In case you’re
wondering, pursuit curves originate from a calculus problem where one
point is in pursuit of another. But don’t worry, the math used in this
assignment will not stray from essential geometric skills, and we’ll
provide a reference to guide you in the calculations. In essence, you’ll
start by drawing a single square of 1 color, then move slightly and turn
inwards by an angle offset, and finally begin drawing another square with a
smaller side length. We note that this is tougher than the first milestone
and very different in the approach because you’ll start with the largest
square and work inwards as each square gets smaller.
To help you get started, here’s the pseudocode for the algorithm:
establish variables for “side length” and “length offset percent”
loop until the length is smaller than 15:
change the turtle color to a new random color
draw a square
calculate the length offset, angle offset, and new side length*
set up for the next square*
Using the above pseudocode, you’ll have to use your knowledge of for and while loops, random
colors, and turtle movement to complete each step. Note that the “length offset percent” represents
the percent of the current side length you’ll move to start drawing the next square. Crucially, we
placed “*” next to denote the two trickiest steps in the algorithms. These steps require precise
geometry and adjustments to get the pursuit curves visual correct. On the next page, we lay out the
precise math that you’ll need to calculate the length offset and new side length as well as set up for
the next square.
Now, we’ll focus on the two tricky steps mentioned above. Below, you’ll see the beginning to the
visual you’ll create (at left) and a zoomed in version focusing on the math we need to go from one
step to the next.
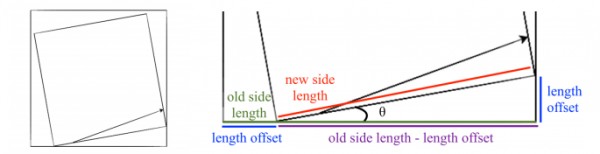
Above, we see several variables. In green, we have the old side length. In red, we have the new side
length, and in blue, we have the length offset, both of which we’ll need to calculate in code. Lastly,
in purple, we have the old side length minus the length offset. We also have noted the angle offset as θ.
To calculate the new side length and length offset, we need to perform the following steps:
1. To calculate the length offset, we multiple the old side length by the “length offset percent”
variable. As mentioned above, the length offset percent can be thought of the percent of the
old side length that will be the length offset. For example, if “length offset perfect” = 0.10
and the old side length is 100, then the length offset should be 10.
2. To calculate the offset angle θ, we’ll need to use a trigonometry functions called arctangent,
which helps to calculate a triangle angle given two side lengths. To find θ, we can perform
the following math:
To do this, you’ll want to use the math.atan(x) function. Important note: the output of the
atan (or arctan) function will be in radians. This is another way to represent degrees, and
we’ll show you how to convert back to degrees in step 4.
3. To calculate the new side length, we’ll need to use another trigonometry function called
cosine. We can find the new side length
To do this, you’ll want to use the math.cos(x) function, where x is an angle in radians.
There is another way to do this using math.sin(x), and either is acceptable.
4. To set up for the next square, you’ll need to move your turtle forward by the offset length
and then turn left by the offset angle. However, as mentioned in step (2), we need to convert
our angle into degrees to turn with turtle. To do that you can do angle_in_degrees = (θ *
180 / math.pi).
