Everything You Need To Know About Sorting Algorithms In C

This article will will put forth an interesting and an important topic that is Sorting Algorithms In C.Following pointers will be covered in this article,

• Bubble Sort
• Insertion Sort
• Selection Sort
• Quick Sort
• Merge Sort

In simple word, sorting means arranging the given elements or data in an ordered sequence. The main purpose of sorting is to easily & quickly locate an element in a sorted list & design an efficient algorithm around it. In this blog we will understand different sorting algorithms & how to implement them in C.

So let us get started then,

Bubble Sort

Bubble Sort is a simple sorting algorithm which repeatedly compares the adjacent elements of the given array & swaps them if they are in wrong order.
Suppose we have an array X which contains n elements which needs to be sorted using Bubble Sort. The sorting works as:

Pass 1:

•  X[0] & X[1] are compared, and swapped if X[0] > X[1]
•  X[1] & X[2] are compared, and swapped if X[1] > X[2]
•  X[2] & X[3] are compared, and swapped if X[2] > X[3] and so on…

At the end of pass 1, the largest element of the list is placed at the highest index of the list.

Pass 2:

• X[0] & X[1] are compared, and swapped if X[0] > X[1]
• X[1] & X[2] are compared, and swapped if X[1] > X[2]
• X[2] & X[3] are compared, and swapped if X[2] > X[3] and so on…

At the end of Pass 2 the second largest element of the list is placed at the second highest index of the list.

Pass n-1:

• X[0] & X[1] are compared, and swapped if X[0] > X[1]
• X[1] & X[2] are compared, and swapped if X[1] > X[2]
• X[2] & X[3] are compared, and swapped if X[2] > X[3] and so on…

At the end of this pass. The smallest element of the list is placed at the first index of the list.

Moving on with this article on Sorting Algorithms In C,

Bubble Sort Program in C

#include <stdio.h> 
// Function to swap elements 
void swap(int *a, int *b) 
{ 
int temp = *a; 
*a = *b; 
*b = temp; 
}  
// bubble sort function
void bubbleSort(int array[], int n) 
{ 
int i, j; 
for (i = 0; i < n-1; i++)       
for (j = 0; j < n-i-1; j++) if (array[j] > array[j+1]) 
swap(&array[j], &array[j+1]); 
}   
// Function to print the elements of an array
void printArray(int array[], int size) 
{ 
int i; 
for (i=0; i < size; i++) 
printf("%d ", array[i]); 
printf("n"); 
}   
// Main Function
int main() 
{ 
int array[] = {89, 32, 20, 113, -15}; 
int size = sizeof(array)/sizeof(array[0]); 
bubbleSort(array, size); 
printf("Sorted array: n"); 
printArray(array, size); 
return 0; 
}

Output:

Moving on with this article on Sorting Algorithms In C,

Insertion Sort

Insertion Sort is a sorting algorithm where the array is sorted by taking one element at a time. The principle behind insertion sort is to take one element, iterate through the sorted array & find its correct position in the sorted array.

Step 1 − If the element is the first one, it is already sorted.
Step 2 – Move to next element
Step 3 − Compare the current element with all elements in the sorted array
Step 4 – If the element in the sorted array is smaller than the current element, iterate to the next element. Otherwise, shift all the greater element in the array by one position towards right
Step 5 − Insert the value at the correct position
Step 6 − Repeat until the complete list is sorted

Insertion Sort Program in C

#include <math.h> 
#include <stdio.h>   
// Insertion Sort Function
void insertionSort(int array[], int n) 
{ 
int i, element, j; 
for (i = 1; i < n; i++) { element = array[i]; j = i - 1; while (j >= 0 && array[j] > element) { 
array[j + 1] = array[j]; 
j = j - 1; 
} 
array[j + 1] = element; 
} 
}   
// Function to print the elements of an array
void printArray(int array[], int n) 
{ 
int i; 
for (i = 0; i < n; i++) 
printf("%d ", array[i]); 
printf("n"); 
}  
// Main Function 
int main() 
{ 
int array[] = { 122, 17, 93, 3, 56 }; 
int n = sizeof(array) / sizeof(array[0]); 
insertionSort(array, n); 
printArray(array, n); 
return 0; 
}

Output

Moving on with this article on Sorting Algorithms In C,

Selection Sort

Selection Sort repeatedly searches for the smallest element from the unsorted part of the array and places it at the end of sorted part of the array. Selection sort first finds the smallest element in the unsorted array and swaps it with the first element. Then it finds the second smallest element in the unsorted array and swaps it with the second element, and the algorithm keeps doing this until the entire array is sorted.

Selection Sort Program in C

#include <stdio.h>  
// Function to swap elements
void swap(int *a, int *b) 
{ 
int temp = *a; 
*a = *b; 
*b = temp; 
}   
// Selection Sort
void selectionSort(int array[], int n) 
{ 
int i, j, min_element; 
for (i = 0; i < n-1; i++) 
{
min_element = i; 
for (j = i+1; j < n; j++) 
if (array[j] < array[min_element]) 
min_element = j; 
swap(&array[min_element], &array[i]); 
} 
}   
// Function to print the elements of an array
void printArray(int array[], int size) 
{ 
int i; 
for (i=0; i < size; i++) 
printf("%d ", array[i]); 
printf("n"); 
}   
// Main Function
int main() 
{ 
int array[] = {15, 10, 99, 53, 36}; 
int size = sizeof(array)/sizeof(array[0]); 
selectionSort(array, size); 
printf("Sorted array: n"); 
printArray(array, size); 
return 0; 
}

Output

Moving on with this article on Sorting Algorithms In C,

Quick Sort

QuickSort is a divide & conquer algorithm. QuickSort algorithm partitions the complete array around the pivot element. Pivot element can be picked in mulitple ways:

• First element as pivot
• Last element as pivot
• Median element as pivot
• Random element as pivot

In this blog we will be picking the last element as pivot element.
partition() is the key process behind the QuickSort algorithm. In partitioning, the pivot element plays an important role. Pivot is placed at its correct position in the sorted array, all the elements smaller than pivot is placed before it, and all the elements greater than pivot is placed after it. All this operation is completed in linear time.
Then the array is divided in two parts from the pivot element (i.e. elements less than pivot & elements greater than pivot) & both the arrays are recursively sorted using Quicksort algorithm.

Moving on with this article on Sorting Algorithms In C,

Quicksort Program in C

#include<stdio.h>  
// Function to swap two elements 
void swapElements(int* x, int* y) 
{ 
int temp = *x; 
*x = *y; 
*y = temp; 
}   
// Partition function
int partition (int arr[], int lowIndex, int highIndex) 
{ 
int pivotElement = arr[highIndex];
int i = (lowIndex - 1); 
for (int j = lowIndex; j <= highIndex- 1; j++) 
{ 
if (arr[j] <= pivotElement) 
{ 
i++; 
swapElements(&arr[i], &arr[j]); 
} 
} 
swapElements(&arr[i + 1], &arr[highIndex]); 
return (i + 1); 
}   
// QuickSort Function
void quickSort(int arr[], int lowIndex, int highIndex) 
{ 
if (lowIndex < highIndex) 
{ 
int pivot = partition(arr, lowIndex, highIndex); 
// Separately sort elements before & after partition 
quickSort(arr, lowIndex, pivot - 1); 
quickSort(arr, pivot + 1, highIndex); 
} 
}   
// Function to print array
void printArray(int arr[], int size) 
{ 
int i; 
for (i=0; i < size; i++) 
printf("%d ", arr[i]); 
}   
// Main Function 
int main() 
{ 
int arr[] = {81, 27, 38, 99, 51, 5}; 
int n = sizeof(arr)/sizeof(arr[0]); 
quickSort(arr, 0, n-1); 
printf("Sorted array: "); 
printArray(arr, n); 
return 0; 
}

Output:

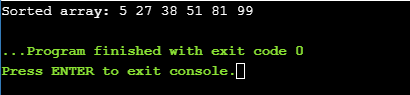
Moving on with this article on Sorting Algorithms In C,

Merge Sort

Merge Sort is one of the best examples of Divide & Conquer algorithm. In Merge sort, we divide the array recursively in two halves, until each sub-array contains a single element, and then we merge the sub-array in a way that it results into a sorted array. merge() function merges two sorted sub-arrays into one, wherein it assumes that array[l .. n] and arr[n+1 .. r] are sorted.

Merge Sort Program in C

#include<stdlib.h> 
#include<stdio.h> 
// Merge Function
void merge(int arr[], int l, int m, int r) 
{ 
int i, j, k; 
int n1 = m - l + 1; 
int n2 =  r - m; 
int L[n1], R[n2]; 
for (i = 0; i < n1; i++) 
L[i] = arr[l + i]; 
for (j = 0; j < n2; j++) 
R[j] = arr[m + 1+ j]; 
i = 0; 
j = 0; 
k = l; 
while (i < n1 && j < n2) 
{ 
if (L[i] <= R[j]) 
{ 
arr[k] = L[i]; 
i++; 
} 
else
{ 
arr[k] = R[j]; 
j++; 
} 
k++; 
} 
while (i < n1) 
{ 
arr[k] = L[i]; 
i++; 
k++; 
} 
while (j < n2) 
{ 
arr[k] = R[j]; 
j++; 
k++; 
} 
}
// Merge Sort Function in C 
void mergeSort(int arr[], int l, int r) 
{ 
if (l < r) 
{ 
int m = l+(r-l)/2; 
mergeSort(arr, l, m); 
mergeSort(arr, m+1, r); 
merge(arr, l, m, r); 
} 
} 
// Functions to Print Elements of Array
void printArray(int A[], int size) 
{ 
int i; 
for (i=0; i < size; i++) 
printf("%d ", A[i]); 
printf("n"); 
}   
// Main Method
int main() 
{ 
int arr[] = {85, 24, 63, 45, 17, 31, 96, 50}; 
int arr_size = sizeof(arr)/sizeof(arr[0]); 
printf("Given array is n"); 
printArray(arr, arr_size); 
mergeSort(arr, 0, arr_size - 1); 
printf("nSorted array is n"); 
printArray(arr, arr_size); 
return 0; 
}

Output:

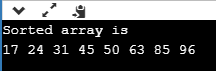
Now after going through the above sorting programs you would have understood various sorting algorithms and how to implement them in C language. I hope this blog is informative and added value to you.

Now after executing the above program you would have understood the Sorting Algorithms In C. Thus we have come to an end of this article on ‘Quicksort in Java’. If you wish to learn more, check out the Java Training by Edureka, a trusted online learning company. Edureka’s Java J2EE and SOA training and certification course is designed to train you for both core and advanced Java concepts along with various Java frameworks like Hibernate & Spring.

Got a question for us? Please mention it in the comments section of this blog and we will get back to you as soon as possible.