Data Science and Machine Learning Internship ...
- 22k Enrolled Learners
- Weekend/Weekday
- Live Class
In simple words, recursion is a way of solving the problem by having a function call itself, The word “recursive” originates from the Latin verb “recurrere”, which means to redo something. This is what the recursive function does, it redoes the same thing again and again, i.e it recalls itself. In this article, we will learn about recursion in python. Following are the topics covered in this blog:
Recursion is the process of determining something in terms of itself. We know that in Python, any function can call any other function, a function can also call itself. These types of functions which call itself till the certain condition is not met are termed as recursive functions.
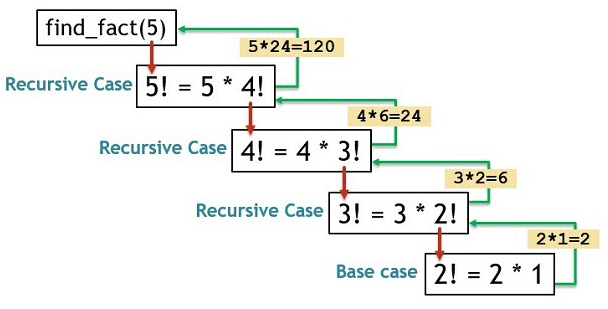
let’s take a few examples to see how that works, If you are given a positive integer n the factorial would be.
Replacing the above values will result in the following expression
We have to define a function lets say fact(n) which takes positive integer or 0 as its parameter and returns the nth factorial, how can we do that using recursion?
Let’s see, to do so using recursion we need to examine the following equation
n! = n.(n-1).(n-2)…3.2.1
n! = n.(n-1)! #we can rewrite the above statement as on this line
Now here if we pass 2 as parameter we will get:
2! = 2.1! = 2
Similarly, if we pass 1 we will get:
1! = 1.0! = 1
But if we pass 0, it breaks
0! = 0.(-1)! and here factorial for -1 is not defined so this works only for values > 0
So we have to write two cases
This is a complete solution for all positive integers and 0.
A recursive function has to fulfill an important condition to terminate. Moving towards a condition where the problem can be solved without further recursion, a recursive function will terminate, minimizing the problem into the smaller sub-steps. A recursion can end up in an infinite loop if the condition of termination is not met in the calls.
Factorial conditions:
We will convert the above factorial conditions in python code:
def fact(n):
if n == 1:
return n
else:
return n * fact(n-1)
Let’s take an example, say we want to find factorial of 4:
fact(4) #this will return 4 * fact(3) and so on until n == 1.
Output: 24
It’s used so often as an example for recursion because of its simplicity and clarity. Solving smaller instances of a problem at each step it termed as recursion in computer science.
In some languages, you can create an infinite recursive loop but, in Python, there is a recursion limit. To check the limit run the following function from sys module. which will give the limit of the recursion set for python.
import sys sys.getrecursionlimit()
Output: 1000
You can also change the limit using the sys module’s functionsetrecursionlimit() according to your requirement, Now let’s create a function which is calling itself recursively till it exceeds the limit and checks what happens:
def recursive():
recursive()
if __name__ == '__main__':
recursive()
If you run the above code, you will get a runtime exception : RuntimeError: maximum recursion depth exceeded. Python prevents you from creating a function that ends up in a never-ending recursive loop.
Other things you can do using recursion except for factorials, let’s say you want to create single from a list which is nested, it can be done using the code below:
def flatten(a_list , flat_list=none):
if flat_list is none:
flat_list = []
for item in a_list:
if isinstance(item, list):
flatten(item , flat_list)
else:
flat_list.append(item)
return flat_list
if __name__ == '__main__':
nested = [1,2,3,[4,5] , 6]
x = flatten(nested)
print(x)
Output: [1,2,3,4,5,6]
Running the above code will result in a single list instead of integer list containing integer list which we used as input. You can also do the same thing using other ways as well, Python has something called itertools.chain() you can check the code used for creating a function chain() it is a different approach to do the same thing as we did.
The code is clean and elegant in a recursive function.
A composite task can be broken down into simpler sub-problems using recursion.
Generating sequence is easier with recursion than using some nested iteration.
Following the logic behind recursive function might be hard sometimes.
Recursive calls are expensive (inefficient) as they take up a lot of memory and time.
Recursive functions are hard to debug.
In this article we saw what recursion is and how can we develop recursive functions from the problem statement, how mathematically a problem statement can be defined. We solved a problem of the factorial and found out conditions required to find factorials from which we were able to convert that conditions into python code giving you the understanding of how recursion works. I think it’s neat that Python has a built-in limit for recursion to prevent developers from creating poorly constructed recursive functions. One important thing to notice is that recursion is hard to debug as the function keeps calling itself.
| Course Name | Date | Details |
|---|---|---|
| Python Programming Certification Course | Class Starts on 27th July,2024 27th July SAT&SUN (Weekend Batch) | View Details |
| Python Programming Certification Course | Class Starts on 31st August,2024 31st August SAT&SUN (Weekend Batch) | View Details |
| Python Programming Certification Course | Class Starts on 28th September,2024 28th September SAT&SUN (Weekend Batch) | View Details |
 REGISTER FOR FREE WEBINAR
REGISTER FOR FREE WEBINAR  Thank you for registering Join Edureka Meetup community for 100+ Free Webinars each month JOIN MEETUP GROUP
Thank you for registering Join Edureka Meetup community for 100+ Free Webinars each month JOIN MEETUP GROUP
edureka.co
