How to Implement Matrices in Python using NumPy?

Matrices are used as a mathematical tool for a variety of purposes in the real world. In this article, we will discuss everything there is about Matrices in Python using the famous NumPy library in the following order:

• What is NumPy and when to use it?
• Creating a Matrix in NumPy
• Matrix operations and examples
• Slicing of Matrices

BONUS: Putting It All Together – Python Code to Solve a System of Linear Equations

Let’s get started with Matrices in Python.

What is NumPy and when to use it?

NumPy is a Python library allowing easy numerical calculations involving single and multidimensional arrays and matrices. As the name suggests, NumPy excels in performing numerical calculations. Many data science libraries like Pandas, Scikit-learn, SciPy, matplotlib, etc. depend on NumPy. It forms an integral part of today’s data science applications written in Python.

Many linear algebra calculations become easy to solve using NumPy. Linear algebra is the core mathematical tool used in many Machine Learning algorithms. Hence knowing NumPy in detail helps you in creating libraries or extend existing Machine Learning libraries.

NumPy provides:

• a powerful N-dimensional array object called as ndarray
• Broadcasting functions
• Tools for integrating C/C++ and Fortran code
• Useful linear algebra, Fourier transform, and random number capabilities

Now let’s move on with our matrices in Python and see how to create a matrix.

Creating a matrix in NumPy

Creating a matrix using lists

## Import numpy
import numpy as np

## Create a 2D numpy array using python lists
arr = np.array([[ 1, 2, 3],[ 4, 5, 6]])
print(arr)

np.array is used to create NumPy array from a list. NumPy arrays are of type ndarray.

The output of the above program is:

It represents a 2D matrix where input to np.array() is a list of lists [[ 1, 2, 3],[ 4, 5, 6]] . Each list in the parent list forms a row in the matrix.

Creating matrix using ranges

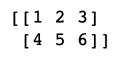
np.arange() can generate a sequence of numbers given the start and end.

## Generate numbers from (start) to (end-1)
## Here start = 0
## end = 5
## Generated a NumPy array from 0 to 4
print(np.arange(0,5))

Above statement outputs the following 1D array:

To generate 2D matrix we can use np.arange() inside a list. We pass this list into np.array() which makes it a 2D NumPy array.

print(np.array([np.arange(0,5), np.arange(5,10)]))

Above statement outputs the following 2D array:

Shape of NumPy array

We refer to any NumPy object as an array of N-dimensions. In mathematics it is referred to as matrix of N-dimensions. Every NumPy ndarray object can be queried for its shape. A shape is a tuple of the format (n_rows, n_cols)

Following snippet prints shape of a matrix

## Using example from above section to generate a matrix using ranges
arr_2d = np.array([np.arange(0,5), np.arange(5,10)])
print(arr_2d.shape)

Output:

 (2, 5) means that the matrix has 2 rows and 5 columns

Matrix filled with zeros and ones

Filling with zeros:

## Create a matrix of shape (3, 4) filled wit zeros
## By default float64 type of numbers are generated if not specified
print(np.zeros((3, 4)))

Output:

By default type of numbers are generated in the array is of float64 if not specified.

Filling with ones:

## Create a matrix of shape (2, 2) filled with ones
## Here we have specified dtype = np.int16 which asks NumPy to generate integers
print(np.ones((2, 2), dtype=np.int16))

Output:

There is a twist while generating a matrix with ones, we have passed an additional parameter dtype=np.int16. This forces the np.ones function to generate integers rather than the default float. This additional parameter can also be passed into np.zeros

Matrix Operations and Examples

Addition

The example below explains two types of addition:

• Scalar addition
• Matrix addition

import numpy as np
## Generate two matrices
mat_2d_1 = np.array([np.arange(0,3), np.arange(3,6)])
mat_2d_2 = np.array([np.arange(6,9), np.arange(9,12)])</pre>
print("Matrix1: n ", mat_2d_1)
print("Matrix2: n ", mat_2d_2)

## Add 1 to each element in mat_2d_1 and print it
print("Scalar addition: n ", mat_2d_1 + 1)

## Add two matrices above elementwise
print("Element wise addition of two matrices of same size: n ", mat_2d_1 + mat_2d_2)

Output:

Subtraction

Subtraction is similar to addition. We just need to change the operation from addition to subtraction.

import numpy as np

## Generate two matrices
mat_2d_1 = np.array([np.arange(0,3), np.arange(3,6)])
mat_2d_2 = np.array([np.arange(6,9), np.arange(9,12)])

print("Matrix1: n ", mat_2d_1)
print("Matrix2: n ", mat_2d_2)

## Subtract 1 from each element in mat_2d_1 and print it
print("Scalar addition: n ", mat_2d_1 - 1)

## Subtract two matrices above elementwise
print("Element wise subtraction of two matrices of same size: n ", mat_2d_1 - mat_2d_2)

Output:

Product

Two types of multiplication or product operation can be done on NumPy matrices

• Scalar product: A scalar value is multiplied with all elements of a matrix
• Dot product: This is the product of two matrices as per the rules of matrix multiplication. Refer Matrix Multiplication for rules of matrix multiplication.

import numpy as np

## Generate two matrices of shape (2,3) and (3,2) so that we can find
## dot product
mat_2d_1 = np.array([np.arange(0,3), np.arange(3,6)])
mat_2d_2 = np.array([np.arange(0,2), np.arange(2,4), np.arange(4,6)])

## Print shapes and matrices
print("Matrix1: n ", mat_2d_1)
print("Matrix1 shape: n", mat_2d_1.shape)
print("Matrix2: n ", mat_2d_2)
print("Matrix2 shape: n", mat_2d_2.shape)

## Multiply each element by 2 in mat_2d_1 and print it
print("Scalar Product: n ", mat_2d_1 * 2)

## Find product of two matrices above using dot product
print("Dot Product: n ", np.dot(mat_2d_1, mat_2d_2))

IMPORTANT: Notice carefully that * operator is used for scalar multiplication only. However, for matrix multiplication we use a function np.dot() which takes two NumPy 2D arrays as argument.

Output:

Division

Element wise scalar division can be done using division operator /

import numpy as np

## Generate a matrix of shape (2,3)
mat_2d = np.array([np.arange(0,3), np.arange(3,6)])

## Print the matrix
print("Matrix: n ", mat_2d)

## Element wise division by scalar
print("Scalar Division: n ", mat_2d / 2)

Output:

Exponent

Element wise exponent can be found out using operator **

import numpy as np

## Generate a matrix of shape (2,3)
mat_2d = np.array([np.arange(0,3), np.arange(3,6)])

## Print the matrix
print("Matrix: n ", mat_2d)

## Find exponent element wise i.e. raise each element in matrix to power 2
print("Matrix raised to power of 2: n ", mat_2d ** 2)

Output:

Transpose

• The transpose of a matrix is a new matrix whose rows are the columns of the original
• A (2, 3) matrix becomes (3, 2) matrix in shape
• Numpy has a property on every ndarray object that stores transpose of a matrix. We need not use any special operator to find transpose of a matrix.
• matrix.T provides transpose of a matrix in NumPy
• Below snippet demonstrates transpose operation

import numpy as np

## Generate a matrix of shape (2,3)
mat_2d = np.array([np.arange(0,3), np.arange(3,6)])

## Print the matrix
print("Matrix: n ", mat_2d)

## Matrix Transpose
print("Transpose n ", mat_2d.T)

Output:

Slicing a Matrix

• A matrix slice is selecting a sub-matrix. Python provides a wonderful syntax to index and slice matrices.
• Slicing uses below syntax:

• • matrix[row index range, column index range, step number]
  • Row and column index ranges follow standard python syntax begin index: end index
  • The range selected is always from begin index to (end index – 1) when code is run

Slicing to select a row

import numpy as np
# Create a matrix
mat_2d = np.array([np.arange(0,3), np.arange(3,6)])
print("Matrix: n", mat_2d)

# Slice to get second row in matrix
print("Sliced: n ", mat_2d[1:, :])

Output:

• IMPORTANT:

• • The row range selection 1: means select row index 1 until the last row
  • The column range index : means select all columns in selected row range

Slicing to select a column

import numpy as np
# Create a matrix
mat_2d = np.array([np.arange(0,3), np.arange(3,6)])
print("Matrix: n", mat_2d)

# Slice to get last column in matrix
print("Sliced: n ", mat_2d[:, 2:])

Output:

• IMPORTANT:

• • The row range selection : means select all rows
  • The column range index 2: means select all columns beginning from index 2 till the end

Slicing to select a sub-matrix

import numpy as np
# Create a matrix
mat_2d = np.array([np.arange(0,4), np.arange(4,8), np.arange(8,12), np.arange(12,16)])
print("Matrix: n", mat_2d)

# Slice to get (2, 2) submatrix in the centre of mat_2d
# i.e.
# [ [ 5 6]
# [ 9 10] ]
print("Sliced: n ", mat_2d[1:3, 1:3])

Output:

• IMPORTANT:

• • The row range selection 1:3 selects rows with index 1 to 2 inclusive
  • The column range selection 1:3 selects columns with index 1 to 2 inclusive

BONUS: Solving Linear System of Equations

System of Equations

• The matrix notation to solve a system of equations is:

• • X = np.dot( (Inverse of A), B)
  • Where:

• • • X = vector of unknows
    • A = Coefficients on LHS
    • B = Values on RHS

• For example, consider below linear system of equations:

• x  + y  + z = 1
  2x + 4y + z = -2
  x  – y  + z = 0
• can be represented in matrices as:
• X = [ x y z] the vector of unknows
  A = [ [1  1 1]
        [2 4 1]
        [1 -1 1] ]
  
  B = [ 1 -2 0 ]

• Using matrix formula mentioned above, we can solve the system of equations as follows:

import numpy as np

## A = (3,3) matrix
A = np.array([[1,1,1], [2,4,1], [1,-1,1]])
## B = (3,1) matrix
B = np.array([1,-2, 0]).T

## X = Inv(A).B = (3, 1) in shape
X = np.dot(np.linalg.inv(A), B)

print("Solution: n ", X)

Output:

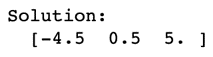
Where, x = -4.5, y = 0.5 and z = 5.0

With this, we have come to the end of our article. I hope you understood what are matrices in Python.

To get in-depth knowledge of Python along with its various applications, you can enroll for live Python certification course online with 24/7 support and lifetime access. 

Got a question for us? Please mention it in the comments section of the ” Matrices in Python” blog and we will get back to you as soon as possible.