Agentic AI Certification Training Course
- 4k Enrolled Learners
- Weekend/Weekday
- Live Class
We are probably living in the most defining period in technology. The period when computing moved from large mainframes to PCs to self-driving cars and robots. But what makes it defining is not what has happened, but what has gone into getting here. What makes this period exciting is the democratization of the resources and techniques. Data crunching which once took days, today takes mere minutes, all thanks to Machine Learning Algorithms.
This is the reason a Data Scientist gets home a whopping $124,000 a year, increasing the demand for Data Science Certifications.
The backbone of modern AI systems is a machine learning algorithm. Those who are looking to master the intricacies of these algorithms. Enrolling MLOps certification course is necessary. It helps to develop, monitor, and effectively maintain the models of ML in the current environment.
Machine Learning is a concept which allows the machine to learn from examples and experience, and that too without being explicitly programmed.
Let me give you an analogy to make it easier for you to understand.
Let’s suppose one day you went shopping for apples. The vendor had a cart full of apples from where you could handpick the fruit, get it weighed and pay according to the rate fixed (per Kg).
Task: How will you choose the best apples?
Given below is set of learning that a human gains from his experience of shopping for apples, you can drill it down to have a further look at it in detail. Go through it once, you will relate it to machine learning very easily.
Learning 1: Bright red apples are sweeter than pale ones
Learning 2: The smaller and bright red apples are sweet only half the time
Learning 3: Small, pale ones aren’t sweet at all
Learning 4: Crispier apples are juicier
Learning 5: Green apples are tastier than red ones
Learning 6: You don’t need apples anymore

Now, imagine you were asked to write a computer program to choose your apples. You might write the following rules/algorithm:
if (bright red) and if (size is big): Apple is sweet.
if (crispy): Apple is juicy
You would use these rules to choose the apples.
But every time you make a new observation (what if you had to choose oranges, instead) from your experiments, you have to modify the list of rules manually.
You have to understand the details of all the factors affecting the quality of the fruit. If the problem gets complicated enough, it might get difficult for you to make accurate rules by hand that covers all possible types of fruit. This will take a lot of research and effort and not everyone has this amount of time.
This is where Machine Learning Algorithms come into the picture.
So instead of you writing the code, what you do is you feed data to the generic algorithm, and the algorithm/machine builds the logic based on the given data.
Find out our Machine Learning Certification Training Course in Top Cities
Machine Learning algorithm is an evolution of the regular algorithm. It makes your programs “smarter”, by allowing them to automatically learn from the data you provide. The algorithm is mainly divided into:
So, building upon the example I had given a while ago, let’s talk a little about these phases.
Training Phase
You take a randomly selected specimen of apples from the market (training data), make a table of all the physical characteristics of each apple, like color, size, shape, grown in which part of the country, sold by which vendor, etc (features), along with the sweetness, juiciness, ripeness of that apple (output variables). You feed this data to the machine learning algorithm (classification/regression), and it learns a model of the correlation between an average apple’s physical characteristics, and its quality.
Testing Phase
Next time when you go shopping, you will measure the characteristics of the apples which you are purchasing(test data)and feed it to the Machine Learning algorithm. It will use the model which was computed earlier to predict if the apples are sweet, ripe and/or juicy. The algorithm may internally use the rules, similar to the one you manually wrote earlier (for eg, a decision tree). Finally, you can now shop for apples with great confidence, without worrying about the details of how to choose the best apples.
Conclusion
You know what! you can make your algorithm improve over time (reinforcement learning) so that it will improve its accuracy as it gets trained on more and more training dataset. In case it makes a wrong prediction it will update its rule by itself.
The best part of this is, you can use the same algorithm to train different models. You can create one each for predicting the quality of mangoes, grapes, bananas, or whichever fruit you want.
For a more detailed explanation on Machine Learning Algorithms feel free to go through this video:
This Machine Learning Algorithms Tutorial shall teach you what machine learning is, and the various ways in which you can use machine learning to solve a problem!
Let’s categorize Machine Learning Algorithm into subparts and see what each of them are, how they work, and how each one of them is used in real life.
So, Machine Learning Algorithms can be categorized by the following three types.

This category is termed as supervised learning because the process of an algorithm learning from the training dataset can be thought of as a teacher teaching his students. The algorithm continuously predicts the result on the basis of training data and is continuously corrected by the teacher. The learning continues until the algorithm achieves an acceptable level of performance. Deep Learning Tutorial guides you through neural networks and advanced models that mimic human brain functionality.
Let me rephrase you this in simple terms:
In Supervised machine learning algorithm, every instance of the training dataset consists of input attributes and expected output. The training dataset can take any kind of data as input like values of a database row, the pixels of an image, or even an audio frequency histogram.
Example: In Biometric Attendance you can train the machine with inputs of your biometric identity – it can be your thumb, iris or ear-lobe, etc. Once the machine is trained it can validate your future input and can easily identify you.
Machine Learning Algorithms: What is Unsupervised Learning?
Well, this category of machine learning is known as unsupervised because unlike supervised learning there is no teacher. Algorithms are left on their own to discover and return the interesting structure in the data.
The goal for unsupervised learning is to model the underlying structure or distribution in the data in order to learn more about the data.
Let me rephrase it for you in simple terms:
In the unsupervised learning approach, the sample of a training dataset does not have an expected output associated with them. Using the unsupervised learning algorithms you can detect patterns based on the typical characteristics of the input data. Clustering can be considered as an example of a machine learning task that uses the unsupervised learning approach. The machine then groups similar data samples and identify different clusters within the data.
Example: Fraud Detection is probably the most popular use-case of Unsupervised Learning. Utilizing past historical data on fraudulent claims, it is possible to isolate new claims based on its proximity to clusters that indicate fraudulent patterns.
Machine Learning Algorithms: What is Reinforcement Learning?
Reinforcement learning can be thought of like a hit and trial method of learning. The machine gets a Reward or Penalty point for each action it performs. If the option is correct, the machine gains the reward point or gets a penalty point in case of a wrong response.
The reinforcement learning algorithm is all about the interaction between the environment and the learning agent. The learning agent is based on exploration and exploitation.
Exploration is when the learning agent acts on trial and error and Exploitation is when it performs an action based on the knowledge gained from the environment. The environment rewards the agent for every correct action, which is the reinforcement signal. With the aim of collecting more rewards obtained, the agent improves its environment knowledge to choose or perform the next action.
Pavlov divided the training of his dog into three stages.
Stage 1: In the first part, Pavlov gave meat to the dog, and in response to the meat, the dog started salivating.
Stage 2: In the next stage he created a sound with a bell, but this time the dogs did not respond to anything.
Stage 3: In the third stage, he tried to train his dog by using the bell and then giving them food. Seeing the food the dog started salivating.
Eventually, the dogs started salivating just after hearing the bell, even if the food was not given as the dog was reinforced that whenever the master will ring the bell, he will get the food. Reinforcement Learning is a continuous process, either by stimulus or feedback.
Here is the list of 5 most commonly used machine learning algorithms.
It is used to estimate real values (cost of houses, number of calls, total sales etc.) based on continuous variables. Here, we establish a relationship between the independent and dependent variables by fitting the best line. This best fit line is known as the regression line and represented by a linear equation Y= aX + b.
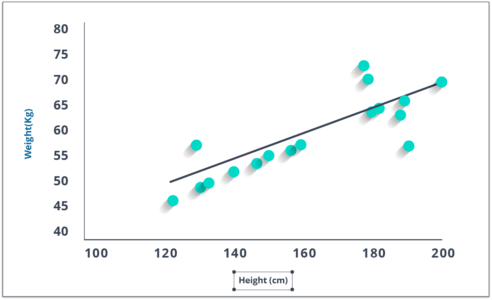
The best way to understand linear regression is to relive this experience of childhood. Let us say, you ask a child in fifth grade to arrange people in his class by increasing order of weight, without asking them their weights! What do you think the child will do? He/she would likely look (visually analyze) at the height and build of people and arrange them using a combination of these visible parameters. This is a linear regression in real life! The child has actually figured out that height and build would be correlated to the weight by a relationship, which looks like the equation above.
In this equation:
These coefficients a and b are derived based on minimizing the ‘sum of squared differences’ of distance between data points and regression line.
Look at the plot given. Here, we have identified the best fit having linear equation y=0.2811x+13.9. Now using this equation, we can find the weight, knowing the height of a person.
#Load Train and Test datasets #Identify feature and response variable(s) and values must be numeric and numpy arrays x_train <- input_variables_values_training_datasets y_train <- target_variables_values_training_datasets x_test <- input_variables_values_test_datasets x <- cbind(x_train,y_train) # Train the model using the training sets and check score linear <- lm(y_train ~ ., data = x) summary(linear) #Predict Output predicted= predict(linear,x_test)
Don’t get confused by its name! It is a classification, and not a regression algorithm. It is used to estimate discrete values ( Binary values like 0/1, yes/no, true/false ) based on a given set of independent variable(s). In simple words, it predicts the probability of occurrence of an event by fitting data to a logit function. Hence, it is also known as logit regression. Since it predicts the probability, its output values lie between 0 and 1.
Again, let us try and understand this through a simple example.
Let’s say your friend gives you a puzzle to solve. There are only 2 outcome scenarios – either you solve it or you don’t. Now imagine, that you are being given a wide range of puzzles/quizzes in an attempt to understand which subjects you are good at. The outcome of this study would be something like this – if you are given a trigonometry based tenth-grade problem, you are 70% likely to solve it. On the other hand, if it is grade fifth history question, the probability of getting an answer is only 30%. This is what Logistic Regression provides you.
Coming to the math, the log odds of the outcome is modeled as a linear combination of the predictor variables.
odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence ln(odds) = ln(p/(1-p)) logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXkAbove, p is the probability of the presence of the characteristic of interest. It chooses parameters that maximize the likelihood of observing the sample values rather than that minimize the sum of squared errors (like in ordinary regression).
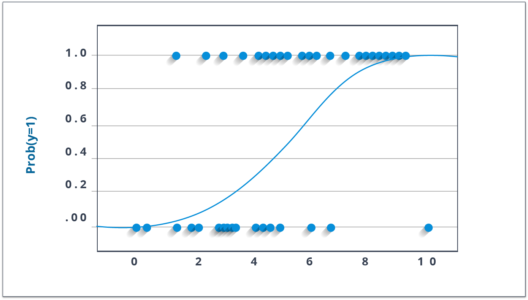 Now, you may ask, why take a log? For the sake of simplicity, let’s just say that this is one of the best mathematical ways to replicate a step function. I can go in more details, but that will beat the purpose of this blog.
Now, you may ask, why take a log? For the sake of simplicity, let’s just say that this is one of the best mathematical ways to replicate a step function. I can go in more details, but that will beat the purpose of this blog.
x <- cbind(x_train,y_train) # Train the model using the training sets and check score logistic <- glm(y_train ~ ., data = x,family='binomial') summary(logistic) #Predict Output predicted= predict(logistic,x_test)
There are many different steps that could be tried in order to improve the model:
Now, this is one of my favorite algorithms. It is a type of supervised learning algorithm that is mostly used for classification problems. Surprisingly, it works for both categorical and continuous dependent variables. In this algorithm, we split the population into two or more homogeneous sets. This is done based on the most significant attributes/ independent variables to make as distinct groups as possible.
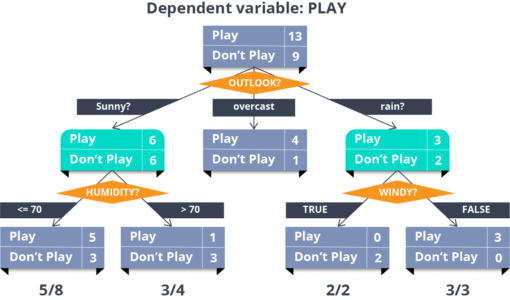
In the image above, you can see that population is classified into four different groups based on multiple attributes to identify ‘if they will play or not’.
library(rpart) x <- cbind(x_train,y_train) # grow tree fit <- rpart(y_train ~ ., data = x,method="class") summary(fit) #Predict Output predicted= predict(fit,x_test)
This is a classification technique based on Bayes’ theorem with an assumption of independence between predictors. In simple terms, a Naive Bayes classifier assumes that the presence of a particular feature in a class is unrelated to the presence of any other feature.
For example, a fruit may be considered to be an apple if it is red, round, and about 3 inches in diameter. Even if these features depend on each other or upon the existence of the other features, a naive Bayes classifier would consider all of these properties to independently contribute to the probability that this fruit is an apple.
Naive Bayesian model is easy to build and particularly useful for very large data sets. Along with simplicity, Naive Bayes is known to outperform even highly sophisticated classification methods.
Bayes theorem provides a way of calculating posterior probability P(c|x) from P(c), P(x) and P(x|c). Look at the equation below:
 Here,
Here,
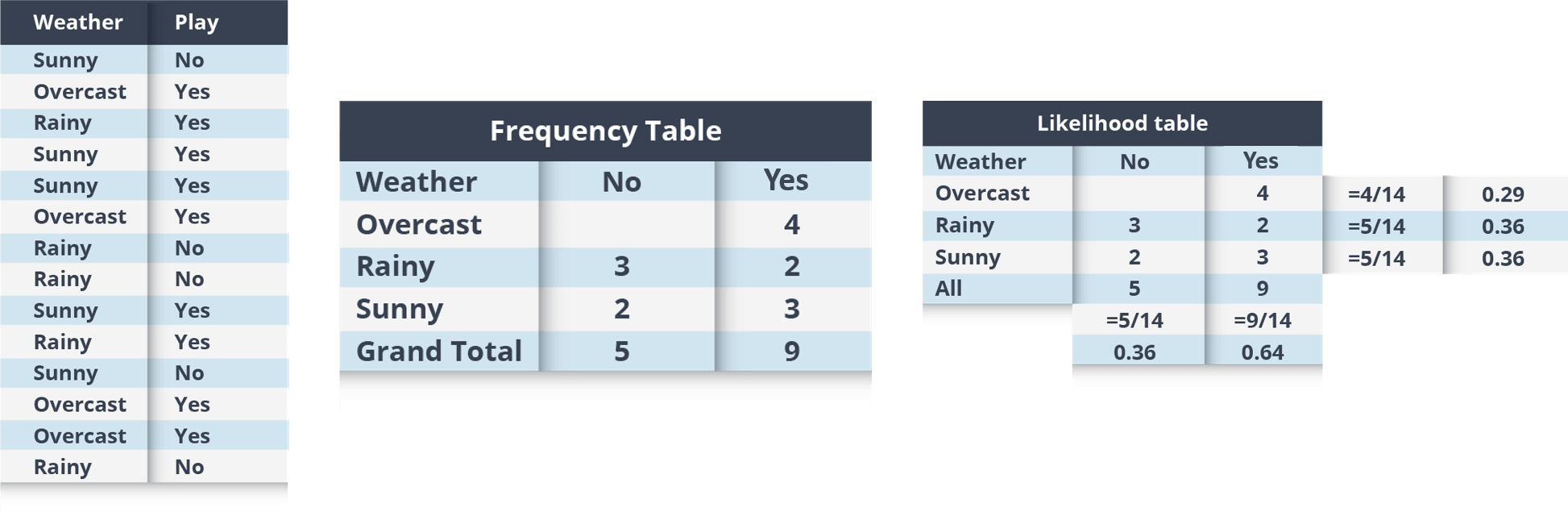
Example: Let’s understand it using an example. Below I have a training data set of weather and corresponding target variable ‘Play’. Now, we need to classify whether players will play or not based on weather condition. Let’s follow the below steps to perform it.
Step 1: Convert the data set to the frequency table
Step 2: Create a Likelihood table by finding the probabilities like Overcast probability = 0.29 and probability of playing is 0.64.
 Step 3: Now, use the Naive Bayesian equation to calculate the posterior probability for each class. The class with the highest posterior probability is the outcome of prediction.
Step 3: Now, use the Naive Bayesian equation to calculate the posterior probability for each class. The class with the highest posterior probability is the outcome of prediction.
Problem: Players will pay if the weather is sunny, is this statement is correct?
We can solve it using above discussed method, so P(Yes | Sunny) = P( Sunny | Yes) * P(Yes) / P (Sunny)
Here we have P (Sunny |Yes) = 3/9 = 0.33, P(Sunny) = 5/14 = 0.36, P( Yes)= 9/14 = 0.64
Now, P (Yes | Sunny) = 0.33 * 0.64 / 0.36 = 0.60, which has higher probability.
Naive Bayes uses a similar method to predict the probability of different class based on various attributes. This algorithm is mostly used in text classification and with problems having multiple classes.
library(e1071) x <- cbind(x_train,y_train) # Fitting model fit <-naiveBayes(y_train ~ ., data = x) summary(fit) #Predict Output predicted= predict(fit,x_test)
It can be used for both classification and regression problems. However, it is more widely used in classification problems in the industry. K nearest neighbors is a simple algorithm that stores all available cases and classifies new cases by a majority vote of its k neighbors. The case being assigned to the class is most common amongst its K nearest neighbors measured by a distance function.
These distance functions can be Euclidean, Manhattan, Minkowski and Hamming distance. First three functions are used for continuous function and the fourth one (Hamming) for categorical variables. If K = 1, then the case is simply assigned to the class of its nearest neighbor. At times, choosing K turns out to be a challenge while performing kNN modeling.
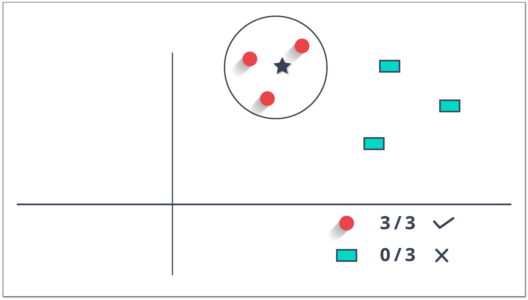
KNN can easily be mapped to our real lives. If you want to learn about a person, of whom you have no information, you might like to find out about his close friends and the circles he moves in and gain access to his/her information!
library(knn) x <- cbind(x_train,y_train) # Fitting model fit <-knn(y_train ~ ., data = x,k=5) summary(fit) #Predict Output predicted= predict(fit,x_test)
This brings me to the end of this blog. Stay tuned for more content on Machine Learning and Data Science!
You can also take a Machine Learning Training Masters Program. The program will provide you with the most in-depth and practical information on machine-learning applications in real-world situations. Additionally, you’ll learn the essentials needed to be successful in the field of machine learning, such as statistical analysis, Python, and data science. The backbone of modern AI systems is a machine learning algorithm. Those who are looking to master the intricacies of these algorithms. Enrolling MLOps training is necessary. It helps to develop, monitor, and effectively maintain the models of ML in the current environment. Machine Learning Tutorial for Beginners introduces core concepts, helping newcomers understand algorithms, data training, and model prediction basics.
 Thank you for registering Join Edureka Meetup community for 100+ Free Webinars each month JOIN MEETUP GROUP
Thank you for registering Join Edureka Meetup community for 100+ Free Webinars each month JOIN MEETUP GROUPedureka.co