K-Nearest Neighbors Algorithm Using Python

What is KNN Algorithm?

kNN is often used in search applications where you are looking for similar items, like find items similar to this one.

Algorithm suggests that if you’re similar to your neighbours, then you are one of them. For example, if apple looks more similar to peach, pear, and cherry (fruits) than monkey, cat or a rat (animals), then most likely apple is a fruit.

How does a KNN Algorithm work?

The k-nearest neighbors algorithm uses a very simple approach to perform classification. When tested with a new example, it looks through the training data and finds the k training examples that are closest to the new example. It then assigns the most common class label (among those k-training examples) to the test example.

What does ‘k’ in kNN Algorithm represent?

If k=1, then test examples are given the same label as the closest example in the training set.

If k=3, the labels of the three closest classes are checked and the most common (i.e., occurring at least twice) label is assigned, and so on for larger ks.

kNN Algorithm Manual Implementation

Let’s consider this example,

Suppose we have height and weight and its corresponding Tshirt size of several customers. Your task is to predict the T-shirt size of Anna, whose height is 161cm and her weight is 61kg.

Step1: Calculate the Euclidean distance between the new point and the existing points

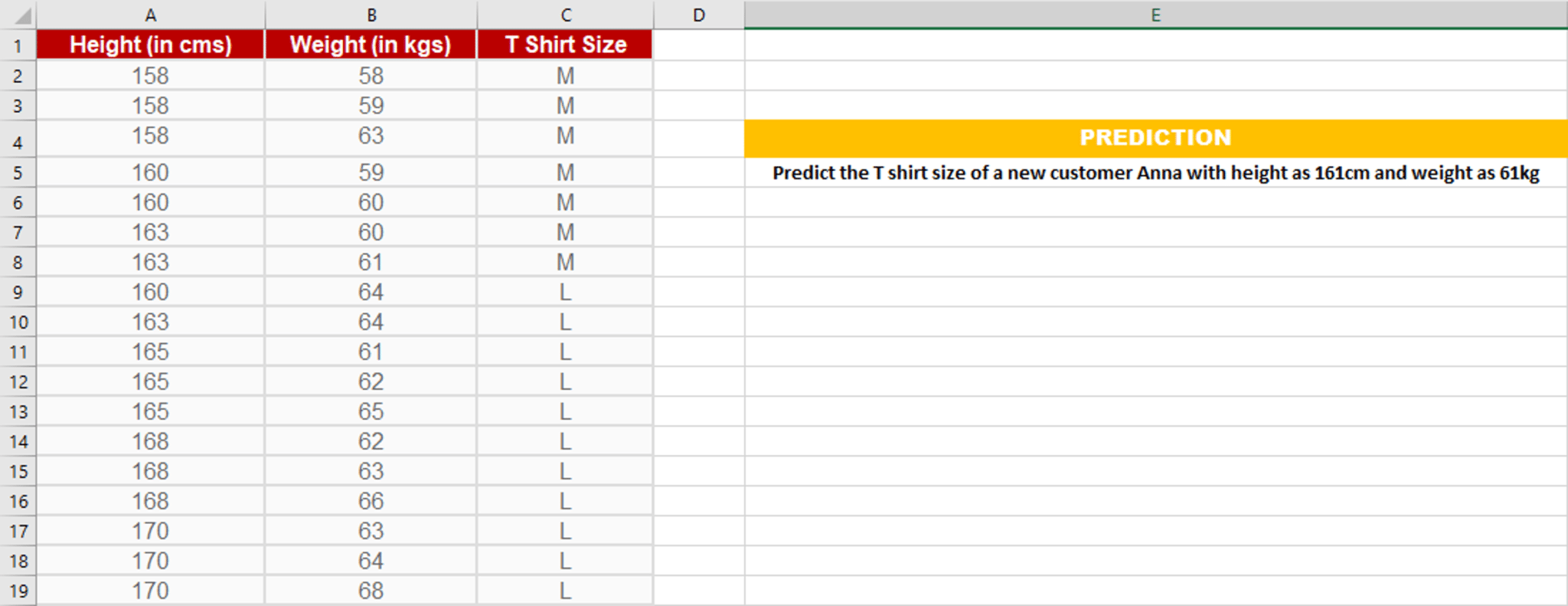
For example, Euclidean distance between point P1(1,1) and P2(5,4) is:

Step 2: Choose the value of K and select K neighbors closet to the new point.

In this case, select the top 5 parameters having least Euclidean distance 

Step 3: Count the votes of all the K neighbors / Predicting Values

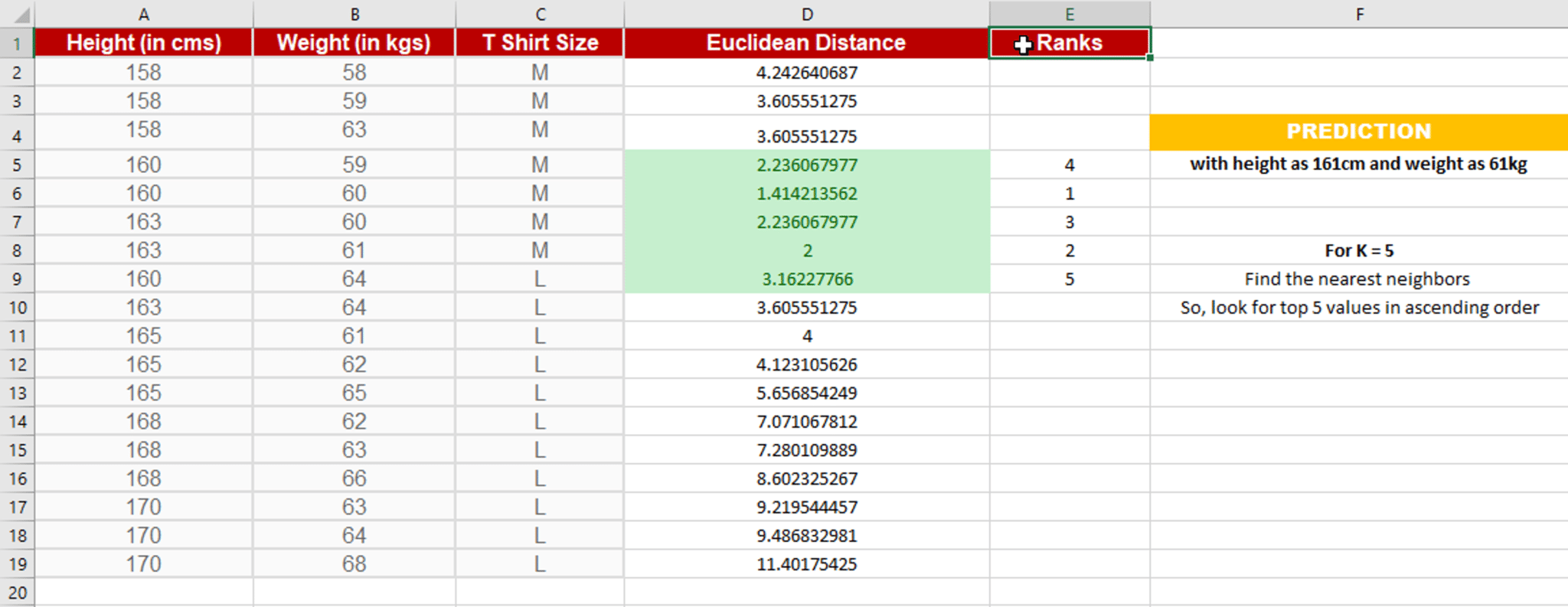
Since for K = 5, we have 4 Tshirts of size M, therefore according to the kNN Algorithm, Anna of height 161 cm and weight, 61kg will fit into a Tshirt of size M.

Implementation of kNN Algorithm using Python

• Handling the data

• Calculate the distance

• Find k nearest point

• Predict the class

• Check the accuracy

Step 1: Handling the data

The very first step will be handling the iris dataset. Open the dataset using the open function and read the data lines with the reader function available under the csv module.

[python]
import csv
with open(r’C:UsersAtul HarshaDocumentsiris.data.txt’) as csvfile:
lines = csv.reader(csvfile)
for row in lines:
print (‘, ‘.join(row))
[/python]

Now you need to split the data into a training dataset (for making the prediction) and a testing dataset (for evaluating the accuracy of the model). 

Before you continue, convert the flower measures loaded as strings to numbers. Next, randomly split the dataset into train and test dataset. Generally, a standard ratio of 67/33 is used for test/train split

Adding it all, let’s define a function handleDataset which will load the CSV when provided with the exact filename and splits it randomly into train and test datasets using the provided split ratio.

[python]
import csv
import random
def handleDataset(filename, split, trainingSet=[] , testSet=[]):
with open(filename, ‘r’) as csvfile:
lines = csv.reader(csvfile)
dataset = list(lines)
for x in range(len(dataset)-1):
for y in range(4):
dataset[x][y] = float(dataset[x][y])
if random.random() < split:
trainingSet.append(dataset[x])
else:
testSet.append(dataset[x])
[/python]

Let’s check the above function and see if it is working fine,

Testing handleDataset function

[python]
trainingSet=[]
testSet=[]
handleDataset(r’iris.data.’, 0.66, trainingSet, testSet)
print (‘Train: ‘ + repr(len(trainingSet)))
print (‘Test: ‘ + repr(len(testSet)))
[/python]

Step 2: Calculate the distance

In order to make any predictions, you have to calculate the distance between the new point and the existing points, as you will be needing k closest points.

In this case for calculating the distance, we will use the Euclidean distance. This is defined as the square root of the sum of the squared differences between the two arrays of numbers

Specifically, we need only first 4 attributes(features) for distance calculation as the last attribute is a class label. So for one of the approach is to limit the Euclidean distance to a fixed length, thereby ignoring the final dimension.

Summing it up let’s define euclideanDistance function as follows:

[python]
import math
def euclideanDistance(instance1, instance2, length):
distance = 0
for x in range(length):
distance += pow((instance1[x] – instance2[x]), 2)
return math.sqrt(distance)
[/python]

Testing the euclideanDistance function,

[python]
data1 = [2, 2, 2, ‘a’]
data2 = [4, 4, 4, ‘b’]
distance = euclideanDistance(data1, data2, 3)
print (‘Distance: ‘ + repr(distance))
[/python]

Step 3: Find k nearest point

Now that you have calculated the distance from each point, we can use it collect the k most similar points/instances for the given test data/instance.

This is a straightforward process: Calculate the distance wrt all the instance and select the subset having the smallest Euclidean distance.

Let’s create a getKNeighbors function that  returns k most similar neighbors from the training set for a given test instance

[python]
import operator
def getKNeighbors(trainingSet, testInstance, k):
distances = []
length = len(testInstance)-1
for x in range(len(trainingSet)):
dist = euclideanDistance(testInstance, trainingSet[x], length)
distances.append((trainingSet[x], dist))
distances.sort(key=operator.itemgetter(1))
neighbors = []
for x in range(k):
neighbors.append(distances[x][0])
return neighbors
[/python]

Testing getKNeighbors function

[python]
trainSet = [[2, 2, 2, ‘a’], [4, 4, 4, ‘b’]]
testInstance = [5, 5, 5]
k = 1
neighbors = getNeighbors(trainSet, testInstance, 1)
print(neighbors)
[/python]

Step 4: Predict the class

Now that you have the k nearest points/neighbors for the given test instance, the next task is to predicted response based on those neighbors

You can do this by allowing each neighbor to vote for their class attribute, and take the majority vote as the prediction.

Let’s create a getResponse function for getting the majority voted response from a number of neighbors.

[python]
import operator
def getResponse(neighbors):
classVotes = {}
for x in range(len(neighbors)):
response = neighbors[x][-1]
if response in classVotes:
classVotes[response] += 1
else:
classVotes[response] = 1
sortedVotes = sorted(classVotes.items(), key=operator.itemgetter(1), reverse=True)
return sortedVotes[0][0]
[/python]

Testing getResponse function

[python]
neighbors = [[1,1,1,’a’], [2,2,2,’a’], [3,3,3,’b’]]
print(getResponse(neighbors))
[/python]

Step 5: Check the accuracy

Now that we have all of the pieces of the kNN algorithm in place. Let’s check how accurate our prediction is!

An easy way to evaluate the accuracy of the model is to calculate a ratio of the total correct predictions out of all predictions made.

Let’s create a getAccuracy function which sums the total correct predictions and returns the accuracy as a percentage of correct classifications.

[python]
def getAccuracy(testSet, predictions):
correct = 0
for x in range(len(testSet)):
if testSet[x][-1] is predictions[x]:
correct += 1
return (correct/float(len(testSet))) * 100.0
[/python]

Testing getAccuracy function

[python]
testSet = [[1,1,1,’a’], [2,2,2,’a’], [3,3,3,’b’]]
predictions = [‘a’, ‘a’, ‘a’]
accuracy = getAccuracy(testSet, predictions)
print(accuracy)
[/python]

Since we have created all the pieces of the KNN algorithm, let’s tie them up using the main function.

[python]
# Example of kNN implemented from Scratch in Python

import csv
import random
import math
import operator

def handleDataset(filename, split, trainingSet=[] , testSet=[]):
with open(filename, ‘rb’) as csvfile:
lines = csv.reader(csvfile)
dataset = list(lines)
for x in range(len(dataset)-1):
for y in range(4):
dataset[x][y] = float(dataset[x][y])
if random.random() < split: trainingSet.append(dataset[x]) else: testSet.append(dataset[x]) def euclideanDistance(instance1, instance2, length): distance = 0 for x in range(length): distance += pow((instance1[x] – instance2[x]), 2) return math.sqrt(distance) def getNeighbors(trainingSet, testInstance, k): distances = [] length = len(testInstance)-1 for x in range(len(trainingSet)): dist = euclideanDistance(testInstance, trainingSet[x], length) distances.append((trainingSet[x], dist)) distances.sort(key=operator.itemgetter(1)) neighbors = [] for x in range(k): neighbors.append(distances[x][0]) return neighbors def getResponse(neighbors): classVotes = {} for x in range(len(neighbors)): response = neighbors[x][-1] if response in classVotes: classVotes[response] += 1 else: classVotes[response] = 1 sortedVotes = sorted(classVotes.iteritems(), key=operator.itemgetter(1), reverse=True) return sortedVotes[0][0] def getAccuracy(testSet, predictions): correct = 0 for x in range(len(testSet)): if testSet[x][-1] == predictions[x]: correct += 1 return (correct/float(len(testSet))) * 100.0 def main(): # prepare data trainingSet=[] testSet=[] split = 0.67 loadDataset(‘iris.data’, split, trainingSet, testSet) print ‘Train set: ‘ + repr(len(trainingSet)) print ‘Test set: ‘ + repr(len(testSet)) # generate predictions predictions=[] k = 3 for x in range(len(testSet)): neighbors = getNeighbors(trainingSet, testSet[x], k) result = getResponse(neighbors) predictions.append(result) print(‘> predicted=’ + repr(result) + ‘, actual=’ + repr(testSet[x][-1]))
accuracy = getAccuracy(testSet, predictions)
print(‘Accuracy: ‘ + repr(accuracy) + ‘%’)

main()
[/python]

This was all about the kNN Algorithm using python. In case you are still left with a query, don’t hesitate in adding your doubt to the blog’s comment section.