Introduction To Markov Chains With Examples – Markov Chains With Python

Introduction To Markov Chains:

Have you ever wondered how Google ranks web pages? If you’ve done your research then you must know that it uses the PageRank Algorithm which is based on the idea of Markov chains. This article on Introduction To Markov Chains will help you understand the basic idea behind Markov chains and how they can be modeled as a solution to real-world problems.

Here’s a list of topics that will be covered in this blog:

1. What Is A Markov Chain?
2. What Is The Markov Property?
3. Understanding Markov Chains With An Example
4. What Is A Transition Matrix?
5. Markov Chain In Python
6. Markov Chain Applications

To get in-depth knowledge on Data Science and Machine Learning using Python, you can enroll for live Data Science Certification Training by Edureka with 24/7 support and lifetime access.

What Is A Markov Chain?

Andrey Markov first introduced Markov chains in the year 1906. He explained Markov chains as:

A stochastic process containing random variables, transitioning from one state to another depending on certain assumptions and definite probabilistic rules.

These random variables transition from one to state to the other, based on an important mathematical property called Markov Property.

This brings us to the question:

What Is The Markov Property?

Discrete Time Markov Property states that the calculated probability of a random process transitioning to the next possible state is only dependent on the current state and time and it is independent of the series of states that preceded it.

The fact that the next possible action/ state of a random process does not depend on the sequence of prior states, renders Markov chains as a memory-less process that solely depends on the current state/action of a variable.

Let’s derive this mathematically:

Let the random process be, {Xm, m=0,1,2,⋯}.

This process is a Markov chain only if,

Markov Chain – Introduction To Markov Chains – Edureka

for all m, j, i, i0, i1, ⋯ im−1

For a finite number of states, S={0, 1, 2, ⋯, r}, this is called a finite Markov chain.

P(Xm+1 = j|Xm = i) here represents the transition probabilities to transition from one state to the other. Here, we’re assuming that the transition probabilities are independent of time.

Which means that P(Xm+1 = j|Xm = i) does not depend on the value of ‘m’. Therefore, we can summarise,

Markov Chain Formula – Introduction To Markov Chains – Edureka

So this equation represents the Markov chain.

Now let’s understand what exactly Markov chains are with an example.

Markov Chain Example

Before I give you an example, let’s define what a Markov Model is:

What Is A Markov Model?

A Markov Model is a stochastic model that models random variables in such a manner that the variables follow the Markov property.

Now let’s understand how a Markov Model works with a simple example.

As mentioned earlier, Markov chains are used in text generation and auto-completion applications. For this example, we’ll take a look at an example (random) sentence and see how it can be modeled by using Markov chains.

Markov Chain Example – Introduction To Markov Chains – Edureka

The above sentence is our example, I know it doesn’t make much sense (it doesn’t have to), it’s a sentence containing random words, wherein:

1. Keys denote the unique words in the sentence, i.e., 5 keys (one, two, hail, happy, edureka)

2. Tokens denote the total number of words, i.e. 8 tokens.

Moving ahead, we need to understand the frequency of occurrence of these words, the below diagram shows each word along with a number that denotes the frequency of that word.

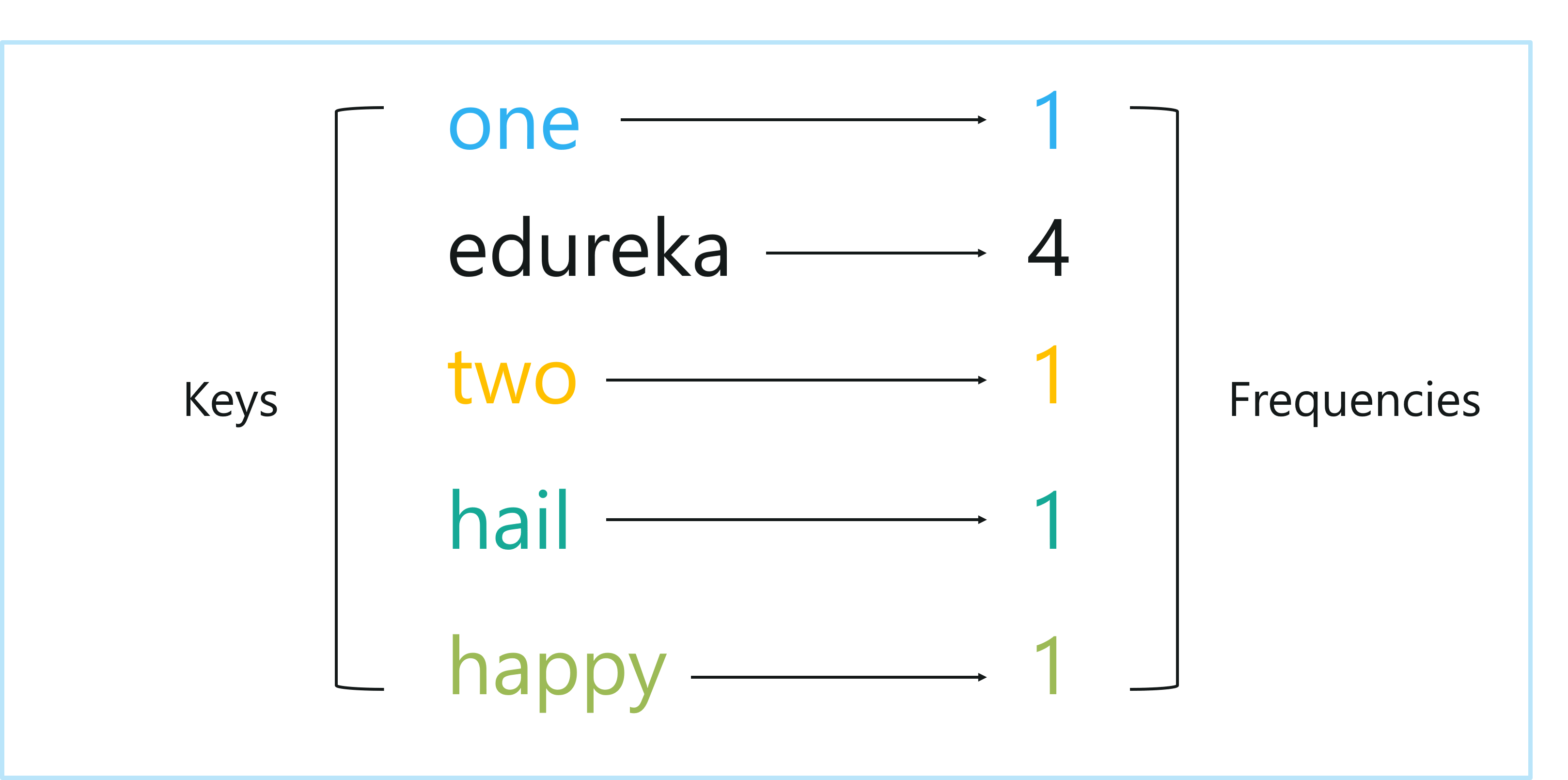
Keys And Frequencies – Introduction To Markov Chains – Edureka

So the left column here denotes the keys and the right column denotes the frequencies.

From the above table, we can conclude that the key ‘edureka’ comes up 4x as much as any other key. It is important to infer such information because it can help us predict what word might occur at a particular point in time. If I were to take a guess about the next word in the example sentence, I would go with ‘edureka’ since it has the highest probability of occurrence.

Speaking about probability, another measure you must be aware of is weighted distributions. 

In our case, the weighted distribution for ‘edureka’ is 50% (4/8) because its frequency is 4, out of the total 8 tokens. The rest of the keys (one, two, hail, happy) all have a 1/8th chance of occurring (≈ 13%).

Now that we have an understanding of the weighted distribution and an idea of how specific words occur more frequently than others, we can go ahead with the next part.

Understanding Markov Chains – Introduction To Markov Chains – Edureka

In the above figure, I’ve added two additional words which denote the start and the end of the sentence, you will understand why I did this in the below section.

Now let’s assign the frequency for these keys as well:

Updated Keys And Frequencies – Introduction To Markov Chains – Edureka

Now let’s create a Markov model. As mentioned earlier, a Markov model is used to model random variables at a particular state in such a way that the future states of these variables solely depends on their current state and not their past states.

So basically in a Markov model, in order to predict the next state, we must only consider the current state.

In the below diagram, you can see how each token in our sentence leads to another one. This shows that the future state (next token) is based on the current state (present token). So this is the most basic rule in the Markov Model.

The below diagram shows that there are pairs of tokens where each token in the pair leads to the other one in the same pair.

Markov Chain Pairs – Introduction To Markov Chains – Edureka

In the below diagram, I’ve created a structural representation that shows each key with an array of next possible tokens it can pair up with. 

An array of Markov Chain Pairs – Introduction To Markov Chains – Edureka

To summarize this example consider a scenario where you will have to form a sentence by using the array of keys and tokens we saw in the above example. Before we run through this example, another important point is that we need to specify two initial measures:

1. An initial probability distribution ( i.e. the start state at time=0, (‘Start’ key))

2. A transition probability of jumping from one state to another (in this case, the probability of transitioning from one token to the other)

We’ve defined the weighted distribution at the beginning itself, so we have the probabilities and the initial state, now let’s get on with the example.

• So to begin with the initial token is [Start]

• Next, we have only one possible token i.e. [one]

• Currently, the sentence has only one word, i.e. ‘one’

• From this token, the next possible token is [edureka]

• The sentence is updated to ‘one edureka’

• From [edureka] we can move to any one of the following tokens [two, hail, happy, end]

• There is a 25% chance that ‘two’ gets picked, this would possibly result in forming the original sentence (one edureka two edureka hail edureka happy edureka). However, if ‘end’ is picked then the process stops and we will end up generating a new sentence, i.e., ‘one edureka’.

Give yourself a pat on the back because you just build a Markov Model and ran a test case through it. To summarise the above example, we basically used the present state (present word) to determine the next state (next word). And that’s exactly what a Markov process is.

It is a stochastic process wherein random variables transition from one state to the other in such a way that the future state of a variable only depends on the present state.

Let’s take it to the next step and draw out the Markov Model for this example.

State Transition Diagram – Introduction To Markov Chains – Edureka

The above figure is known as the State Transition Diagram. We’ll talk more about this in the below section, for now just remember that this diagram shows the transitions and probability from one state to another.

Notice that each oval in the figure represents a key and the arrows are directed toward the possible keys that can follow it. Also, the weights on the arrows denote the probability or the weighted distribution of transitioning from/to the respective states.

So that was all about how the Markov Model works. Now let’s try to understand some important terminologies in the Markov Process.

What Is A Transition Probability Matrix?

In the above section we discussed the working of a Markov Model with a simple example, now let’s understand the mathematical terminologies in a Markov Process.

In a Markov Process, we use a matrix to represent the transition probabilities from one state to another. This matrix is called the Transition or probability matrix. It is usually denoted by P.

Transition Matrix – Introduction To Markov Chains – Edureka

Note, pij≥0, and ‘i’ for all values is,

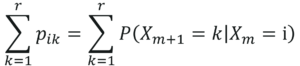
Transition Matrix Formula – Introduction To Markov Chains – Edureka

Let me explain this. Assuming that our current state is ‘i’, the next or upcoming state has to be one of the potential states. Therefore, while taking the summation of all values of k, we must get one.

What Is A State Transition Diagram?

A Markov model is represented by a State Transition Diagram. The diagram shows the transitions among the different states in a Markov Chain. Let’s understand the transition matrix and the state transition matrix with an example.

Transition Matrix Example

Consider a Markov chain with three states 1, 2, and 3 and the following probabilities:

Transition Matrix Example – Introduction To Markov Chains – Edureka

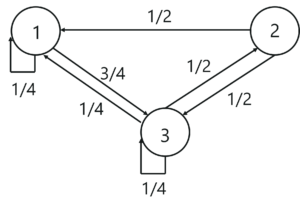
State Transition Diagram Example – Introduction To Markov Chains – Edureka

The above diagram represents the state transition diagram for the Markov chain. Here, 1,2 and 3 are the three possible states, and the arrows pointing from one state to the other states represents the transition probabilities pij. When, pij=0, it means that there is no transition between state ‘i’ and state ‘j’.

Now that we know the math and the logic behind Markov chains, let’s run a simple demo and understand where Markov chains can be used.

Markov Chain In Python

To run this demo, I’ll be using Python, so if you don’t know Python, you can go through these following blogs:

1. Python Tutorial – A Complete Guide to Learn Python Programming
2. How to Learn Python 3 from Scratch – A Beginners Guide
3. Python Programming Language – Head start With Python Basics
4. A Beginners Guide To Python Functions

Now let’s get started with coding!

Markov Chain Text Generator

Problem Statement: To apply Markov Property and create a Markov Model that can generate text simulations by studying Donald Trump speech data set.

Data Set Description: The text file contains a list of speeches given by Donald Trump in 2016.

Logic: Apply Markov Property to generate Donald’s Trump’s speech by considering each word used in the speech and for each word, create a dictionary of words that are used next.

Step 1: Import the required packages

import numpy as np

Step 2: Read the data set

trump = open('C://Users//NeelTemp//Desktop//demos//speeches.txt', encoding='utf8').read()
#display the data

print(trump)

SPEECH 1 ...Thank you so much. That's so nice. Isn't he a great guy. He doesn't get a fair press; he doesn't get it. It's just not fair. 
And I have to tell you I'm here, and very strongly here, because I have great respect for Steve King and have great respect likewise for Citizens 
United, David and everybody, and tremendous resect for the Tea Party. Also, also the people of Iowa. They have something in common. 
Hard-working people....

Step 3: Split the data set into individual words

corpus = trump.split()

#Display the corpus
print(corpus)

'powerful,', 'but', 'not', 'powerful', 'like', 'us.', 'Iran', 'has', 'seeded', 'terror',...

Next, create a function that generates the different pairs of words in the speeches. To save up space, we’ll use a generator object.

Step 4: Creating pairs to keys and the follow-up words

def make_pairs(corpus):
for i in range(len(corpus) - 1):
yield (corpus[i], corpus[i + 1])
pairs = make_pairs(corpus)

Next, let’s initialize an empty dictionary to store the pairs of words.

In case the first word in the pair is already a key in the dictionary, just append the next potential word to the list of words that follow the word. But if the word is not a key, then create a new entry in the dictionary and assign the key equal to the first word in the pair.

Step 5: Appending the dictionary

word_dict = {}
for word_1, word_2 in pairs:
if word_1 in word_dict.keys():
word_dict[word_1].append(word_2)
else:
word_dict[word_1] = [word_2]

Next, we randomly pick a word from the corpus, that will start the Markov chain.

Step 6: Build the Markov model

#randomly pick the first word
first_word = np.random.choice(corpus)

#Pick the first word as a capitalized word so that the picked word is not taken from in between a sentence
while first_word.islower():

#Start the chain from the picked word
chain = [first_word]

#Initialize the number of stimulated words
n_words = 20

Following the first word, each word in the chain is randomly sampled from the list of words which have followed that specific word in Trump’s live speeches. This is shown in the below code snippet:

for i in range(n_words):
chain.append(np.random.choice(word_dict[chain[-1]]))

Step 7: Predictions

Finally, let’s display the stimulated text.

#Join returns the chain as a string
print(' '.join(chain))

The number of incredible people. And Hillary Clinton, has our people, and such great job. And we won’t be beating Obama

So this is the generated text I got by considering Trump’s speech. It might not make a lot of sense but it is good enough to make you understand how Markov chains can be used to automatically generate texts.

Now let’s look at some more applications of Markov chains and how they’re used to solve real-world problems.

Markov Chain Applications

Here’s a list of real-world applications of Markov chains:

1. Google PageRank: The entire web can be thought of as a Markov model, where every web page can be a state and the links or references between these pages can be thought of as, transitions with probabilities. So basically, irrespective of which web page you start surfing on, the chance of getting to a certain web page, say, X is a fixed probability.

2. Typing Word Prediction: Markov chains are known to be used for predicting upcoming words. They can also be used in auto-completion and suggestions.

3. Subreddit Simulation: Surely you’ve come across Reddit and had an interaction on one of their threads or subreddits. Reddit uses a subreddit simulator that consumes a huge amount of data containing all the comments and discussions held across their groups. By making use of Markov chains, the simulator produces word-to-word probabilities, to create comments and topics.

4. Text generator: Markov chains are most commonly used to generate dummy texts or produce large essays and compile speeches. It is also used in the name generators that you see on the web.

Now that you know how to solve a real-world problem by using Markov Chains, I’m sure you’re curious to learn more. Here’s a list of blogs that will help you get started with other statistical concepts:

1. A Complete Guide To Math And Statistics For Data Science
2. All You Need To Know About Statistics And Probability
3. Python for Data Science – How to Implement Python Libraries

With this, we come to the end of this Introduction To Markov Chains blog. If you have any queries regarding this topic, please leave a comment below and we’ll get back to you.

Stay tuned for more blogs on the trending technologies.

If you are looking for online structured training in Data Science, edureka! has a specially curated Python Data Science Certification Training program which helps you gain expertise in Statistics, Data Wrangling, Exploratory Data Analysis, Machine Learning Algorithms like K-Means Clustering, Decision Trees, Random Forest, Naive Bayes. You’ll learn the concepts of Time Series, Text Mining and an introduction to Deep Learning as well. New batches for this course are starting soon!!