Data Science and Machine Learning Internship ...
- 22k Enrolled Learners
- Weekend/Weekday
- Live Class
The knowledge of Data Structures and Algorithms forms the base to identify programmers giving yet another reason for tech enthusiasts to get a Python Certification. While data structures help in the organization of data, algorithms help find solutions to the unending data analysis problems. So if you are still unaware of Data Structures and Algorithms in Python, here is a detailed article that will help you understand and implement them.
Before moving on, take a look at all the topics discussed in over here:
Lists: Stores indexed elements that are changeable and can contain duplicate items
Tuples: Stores indexed, unchangeable elements that can have duplicate copies
Dictionaries: Store key-value pairs that are changeable
Sets: Contains unordered, unique elements that are mutable
Arrays: Similar to Lists, but store single type of elements
Stack: Linear LIFO (Last-In-First-Out) Data structure
Queues: Linear FIFO (First-In-First-Out) data structure
Trees: Non-Linear data structures having a root and nodes
Linked Lists: Linear data structures that are linked with pointers
Graphs: Store a collection of points or nodes along with edges
Hash Maps: In Python, Hash Maps are the same as Dictionaries
This article on Data Structures and Algorithms in Python will require you to have prior knowledge about Data structures in Python. In case you do not have much idea about it, Data Structure in Python article.
Algorithms are rules or instructions that are formulated in a finite, sequential order to solve problems and get the required results. They give the pseudocode for problems and can be implemented in several languages as they are not language-specific.
How do you Write Algorithms?
Algorithms are generally written as a combination of user-understandable language and some common programming languages. They are commonly written down in steps however, it is not always necessary to do so. There are no distinct rules to formulate algorithms but you will need to keep the following points in mind:
For example, if you have to formulate an algorithm to check if a student has passed in an exam or not, you can follow the given steps:
Step 1: START
Step 2: Declare two variables x, y
Step 3: Store the marks obtained by the student in x
Step 4: Store the minimum passing score in y
Step 5: Check if x is greater than or equal to y. If yes, then return “Pass” else return “Fail”
Step 6: STOP
However, you can manipulate the steps according to your preference. For instance, you can assign the values to the variables in step 2 itself rather than taking steps 3 and 4. This way, a single problem can have multiple solutions and it depends on the problem and the programmer to choose the most feasible and reliable solution.
| Class | Description |
Divide and Conquer | Divides the problem into sub-parts and solves each one separately |
Dynamic Programming | Divides the problem into sub-parts, remembers the results of the sub-parts and applies it to similar ones |
Greedy Algorithms | Involves taking the easiest step while solving a problem without worrying about the complexity of the future steps |
Moving ahead with this Data Structures and Algorithms in Python article lets take a look at some of the important algorithms such as the Tree Traversal Algorithms, Searching Algorithms, Sorting Algorithms, etc.
Trees in Python are non-linear data structures having a root and nodes as mentioned earlier. Tree Traversal refers to visiting each node present in the tree exactly once in order to update or check them. Take a look at the tree shown below:
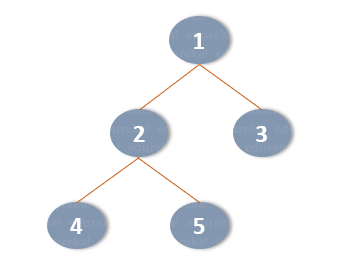
Based on the order in which the nodes are visited, there can be three types of tree traversals:
Before creating functions for each of these traversals, you will need to create a Node class and create the tree using the following piece of code (Run all the functions along with this):
# creating a Node class
class Node:
def __init__(self,val):
self.childleft = None
self.childright = None
self.nodedata = val
# Creating an instance of the Node class to construct the tree shown in the image above
root = Node(1)
root.childleft = Node(2)
root.childright = Node(3)
root.childleft.childleft = Node(4)
root.childleft.childright = Node(5)
In-order traversal refers to traversing the tree in such a way that you first visit the left nodes followed by the root and then right nodes. You begin your traversal from all the nodes in the left subtree, then move towards the root and finally the right subtree.
In the tree shown above 4 is the leftmost node and hence that is the first to be visited. Next, you move towards the root, so the root for node 4 is 2, hence you visit node 2. Following that, you must check if you have any node to the right and the tree shown above, node 5 is present so node5 is visited. Once that is done, the left subtree is completed and then you must follow the same rule again i.e left-root-right in order to complete the traversal.

The algorithm for In-order traversal will be as follows:
Step 1: Traverse through the nodes present in the left subtree
Step 2: Visit the root node
Step 3: Traverse the right subtree
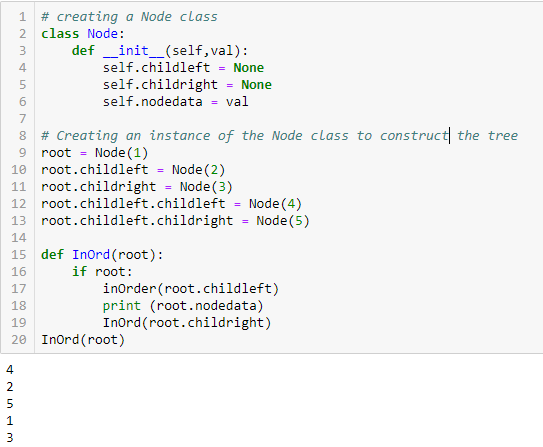
In-order function:
def InOrd(root):
if root:
InOrd(root.childleft)
print (root.nodedata)
InOrd(root.childright)
InOrd(root)When you run this function along with the code shown previously, you will get the In-order traversal for the given binary tree.
In a Pre-Order traversal, the root node is visited first, followed by the left subtree and then the right subtree. So, in the above example, you first visit node 1 followed by node 2 which us towards the left of node 1. Then, you must move towards the left of the node 2 and visit node 4 followed by node 5. With this, the root and left subtree are done and hence, you need to visit the right subtree.

The algorithm for Pre-order traversal will be as follow:
Step 1: Visit the root node
Step 2: Traverse through the nodes present in the left subtree
Step 3: Traverse the right subtree
Pre-Order function:
def PreOrd(root):
if root:
print (root.nodedata)
PreOrd(root.childleft)
PreOrd(root.childright)
PreOrd(root)
Post-order traversal begins from the left then to the right and finally, the root. In the above example, you visit node 4 then move right towards node 5. Once that is done, you must visit the root i.e node 2. With this, the left subtree is complete so you need to move towards the right subtree and finally visit the root.

The algorithm for Post-order traversal will be as follow:
Step 1: Traverse through the nodes present in the left subtree
Step 2: Traverse the right subtree
Step 3: Visit the root node
Post-order function:
def PostOrd(root):
if root:
PostOrd(root.childleft)
PostOrd(root.childright)
print (root.nodedata)
PostOrd(root)Sorting of data is a real-time problem and requires a number of sorting algorithms to be solved. So moving ahead with this Data Structures and Algorithms in Python article, let us take a deep look at the Sorting Algorithms in Python.
Sorting algorithms are used to sort data into some given order. Sorting algorithms can be classified into five types that are:
Note: All algorithms here are sorted in the ascending order.
Merge Sort algorithm follows the Divide and Conquer rule. Here, the given list of items is first divided into smaller lists until it reaches a point where each list consists of exactly one item. By default, a list consisting of one item will be sorted and the merge sort algorithm then compares adjacent lists and reorders them in the desired sequence. This process is done recursively until it reaches a point where there exists only one, sorted list.
Merge Sort Algorithm:
Step 1: Check if the list contains more than one items; if yes, divide the list into two halves, else the list is sorted
Step 2: The list is to be divided repeatedly until there is only a single element left in each sub-list
Step 3: Recursively merge the sub-lists by arranging them in the given order until you get a single sorted list
Merge Sort program:
def msort(mylist, left, right):
if right - left > 1:
middle = (left + right)//2
msort(mylist, left, middle)
msort(mylist, middle, right)
mlist(mylist, left, middle, right)
def mlist(mylist, left, middle, right):
leftlist = mylist[left:middle]
rightlist = mylist[middle:right]
k = left
i = 0
j = 0
while (left + i < middle and middle + j < right):
if (leftlist[i] <= rightlist[j]):
mylist[k] = leftlist[i]
i = i + 1
else:
mylist[k] = rightlist[j]
j = j + 1
k = k + 1
if left + i < middle:
while k < right:
mylist[k] = leftlist[i]
i = i + 1
k = k + 1
else:
while k < right:
mylist[k] = rightlist[j]
j = j + 1
k = k + 1
mylist = input('Enter the list values to be sorted: ').split()
mylist = [int(x) for x in mylist]
msort(mylist, 0, len(mylist))
print('The sorted list is: ')
print(mylist)The above program will allow the user to enter a list that is to be sorted and will display the final sorted list as shown below:
OUTPUT:
Enter the list values to be sorted: 23 1 45 34 7
The sorted list is:
[1, 7, 23, 34, 45]
Bubble sort is a comparison algorithm that first compares and then sorts adjacent elements if they are not in the specified order.
Bubble Sort Algorithm:
Step 1: Beginning from the first element i.e the element at index 0, progressively compare adjacent elements of an array
Step 2: If the current element and the next element are not in the specified order, swap the elements
Step 3: If the current element and the next element are in the specified order, move on to the next element
Bubble Sort Program:
def bs(a): # a = name of list
b=len(a)-1
for x in range(b):
for y in range(b-x):
if a[y]>a[y+1]:
a[y],a[y+1]=a[y+1],a[y]
return a
a=[3,6,1,8]
bs(a)
OUTPUT: [1, 3, 6, 8]
The above program will sort a given list in the ascending order.
Insertion sort picks one element of a given list at a time and places it at the exact spot where it is to be placed.
Insertion Sort Algorithm:
Step 1: Compare the first element with the next element (key) and if the element to the left and the key element are not in order, swap them
Step 2: Take the next element (key) and if the new key element requires to be repositioned, shift the elements of the sorted list towards the right until an appropriate place is created for the element under consideration
Step 3: Repeat step 2 until all elements of the given list are sorted
Insertion Sort Program:
def isort(a):
for x in range(1, len(a)):
k = a[x] #element present at index number 1
j = x-1
while j >=0 and k < a[j] : #comparing elements with the next until the last item
a[j+1] = a[j]
j -= 1 #comparing each element to the elements present to its left
a[j+1] = k #new item becomes the key
a = [24, 56, 1, 50, 17]
isort(a)
print(a)
OUTPUT: [1, 17, 24, 50, 56]
In the above program, the first key element will be 56 and this is compared with 24 which is the first element of the list. Since these two are already sorted, the algorithm accepts the next element i.e 1 and this becomes the new key. Since 1 is smaller than 24 and 56, both 24 and 56 are shifted towards the right and 1 is placed at the beginning of the array. The same procedure is repeated until all the items present in the given array are sorted.
The Selection sort algorithm divides the given list into two halves where the first half will be the sorted list and the second is an unsorted list. At first, the sorted list is empty and all elements to be sorted are present in the unsorted list.
The Selection sort algorithm will look at all the elements present in the unsorted list, pick up the item that is supposed to come first, and then places it in the sorted list. It then repeats the searching process and places the next element to the right of the first element in the sorted list.
For example, if you have to sort the elements in ascending order, the selection sort algorithm will take a look at the complete list, select the smallest element and then places that element as the first element in the sorted list. Then it searches for the next smallest element and places it to the right of the first element and so on.
Selection Sort Algorithm:
Step 1: Make the first element as the minimum and compare it with the next element. If the next element is less than the selected element, mark that as the minimum and compare it with the next element. Repeat the same process until you compare all the elements of the unsorted list
Step 2: Place the minimum in the sorted array (This becomes the first element of the sorted array)
Step 3: Increment the position of the counter to point at the first element of the unsorted array and repeat steps 1 and 2 for all the elements of the unsorted array
Selection Sort Program:
def selsort(myarray, r):
for x in range(r):
minimum = x #first element is assumed to be the minimum
for y in range(x + 1, r):
if myarray[y] < myarray[minimum]: #comparing minimum with the next element
minimum = y
(myarray[x], myarray[minimum]) = (myarray[minimum], myarray[x]) #swap elements if required
mylist = [34, 23, 1, 67, 4]
r = len(mylist)
selsort(mylist, r)
print(mylist)OUTPUT: [1, 4, 23, 34, 67]
The Shell sort algorithm allows you to sort elements that are apart from each other. The original sequence to sort the elements follows n/ 2, n/4, …, 1 sequence where n is the number of elements present in the unsorted list. For example, if you have a list of 8 elements, the length of that list will be divided by 2 i.e 8/ 2 = 4. Now, the first element will be compared with the element present at index number 4 and then, the gap will be produced by dividing 8 by 4. This time, the gap will be 2 and the elements that lie at these intervals will be compared. Finally, 8/ 8 = 1, so adjacent elements will be compared and sorted. (For odd number lists, the whole part of the quotient will be taken as the gap)
Shell Sort Algorithm:
Step 1: Find the value of the gap by dividing the number of elements by 2
Step 2: Divide the given array into smaller sub-arrays having equal gap intervals
Step 3: Using insertion sort, sort the sub-arrays
Step 4: Repeat steps 1, 2 and 3 until the complete array is sorted
Shell Sort Program:
def shsort(myarray, n):
g = n // 2 # dividing the number of elements by 2 to find the gap
while g > 0:
for x in range(g, n):
y = myarray[x]
z = x
while z >= g and myarray[z - g] > y:
myarray[z] = myarray[z - g]
z -= g
myarray[z] = y
g //= 2
mylist = [23, 12, 1, 17, 45, 2, 13]
length = len(mylist)
shsort(mylist, length)
print(mylist)OUTPUT: [1, 2, 12, 13, 17, 23, 45]
Moving ahead with this Data Structures and Algorithms in Python article lets take a look at some of the most important searching algorithms in Python.
Searching algorithms are used to search for or fetch some elements present in some given dataset. There are many types of search algorithms such as Linear Search, Binary Search, Exponential Search, Interpolation search, etc.
The Linear Search algorithm is used to successively search for a given element by comparing it with each element of the given array. It is one of the simplest searching algorithms but very important so as to understand other sorting algorithms.
Linear Search Algorithm:
Step 1: Create a function that will accept the data list, the length of the list and the key element
Step 2: If an element present in the given list matches the key element, return the corresponding index number
Step 3: If the element is not found, return -1
Linear Search Program:
def lin_search(myarray, n, key):
for x in range(0, n):
if (myarray[x] == key):
return x
return -1
myarray = [ 12, 1, 34, 17]
key = 17
n = len(myarray)
matched = lin_search(myarray, n, key)
if(matched == -1):
print("Key is not present")
else:
print("Key is present in the given list at index", matched)OUTPUT: Key is present in the given list at index 3
Binary Search is used to search for some given element in a sorted array by making use of the Decrease and Conquer Algorithm. Here, the key is looked for by first comparing it with the middle element and then dividing the array into half. The left half is searched if the element to be searched for is smaller than the middle element and vice versa. The appropriate sub-arrays are again divided into half and the process is repeated again.
For example, if you have a sorted list of 8 elements, the key element will be compared with the element present at the middle or 7/ 2 = 3.5 (7 is the index value of the last element) and the whole number value is taken for comparison. So, the key element will be compared with the value present at index number 3 and if the given value is smaller, the same process is repeated towards the left side of the middle element and vice versa.
Binary Search Algorithm:
Step 1: Compare the key with the middle element
Step 2: If matched, return the middle index value
Step 3: If the key element is greater than the middle element, search for the key element towards the right of the middle element, else search to the left of it
Binary Search Program:
def bin_search(mylist,key):
l = 0
r = len(mylist)-1
matched = False
while( l<=r and not matched):
middle = (l + r)//2
if mylist[middle] == key :
matched = True
else:
if key < mylist[middle]:
r = middle - 1
else:
l = middle + 1
return matched
print(bin_search([2, 3, 56, 13, 1], 56))
print(bin_search([2, 3, 56, 13, 1], 26))
True
False
The final topic that is discussed in this Data Structures and Algorithms in Python article is Algorithm Analysis.
Algorithms can be analyzed both before and after their implementation. These analyses are referred to as A Priori Analysis and A Posterior Analysis.
A Priori Analysis (Theoretical Analysis): The efficiency of algorithms is measured by presuming that all the other factors are constant and do not affect the implementation of the algorithm.
A Posterior Analysis (Empirical Analysis): The algorithms after being implemented using some programming language, is executed on some computer. So in this analysis, the actual values like time complexity or execution time of an algorithm till it finishes the task, space complexity or the space required by the algorithm for its full life cycle, etc are gathered.
I hope you are clear with all that has been shared with you in this tutorial. This brings us to the end of our article on Data Structures and Algorithms in Python. Make sure you practice as much as possible and revert your experience.
With immense applications and easier implementations of Python with data science, there has been a significant increase in the number of jobs created for data science every year. Enroll for Edureka’s Data Science with Python and get hands-on experience with real-time industry projects along with 24×7 support, which will set you on the path of becoming a successful Data Scientist,
Got a question for us? Please mention it in the comments section of this “Data Structures and Algorithms in Python” blog and we will get back to you as soon as possible.
To get in-depth knowledge of Python along with its various applications, you can enroll for live Python online training with 24/7 support and lifetime access.
| Course Name | Date | Details |
|---|---|---|
| Data Science with Python Certification Course | Class Starts on 3rd August,2024 3rd August SAT&SUN (Weekend Batch) | View Details |
| Data Science with Python Certification Course | Class Starts on 31st August,2024 31st August SAT&SUN (Weekend Batch) | View Details |
| Data Science with Python Certification Course | Class Starts on 28th September,2024 28th September SAT&SUN (Weekend Batch) | View Details |
 REGISTER FOR FREE WEBINAR
REGISTER FOR FREE WEBINAR  Thank you for registering Join Edureka Meetup community for 100+ Free Webinars each month JOIN MEETUP GROUP
Thank you for registering Join Edureka Meetup community for 100+ Free Webinars each month JOIN MEETUP GROUP
edureka.co
