How to write C Program to find the Roots of a Quadratic Equation?

Calculating the roots of a quadratic equation is something that we have learnt in childhood. However, the complexity of quadratic equations increased with time. The methods to deal with this problem have also evolved. In this article, we would take a look a way to write a C program to find the roots of a quadratic equation.

Following are the pointers to be covered in this article:

1. 1. What is a quadratic equation?
   2. Types of roots
   3. Understanding the Algorithm
   4. C program to find the roots of a Quadratic Equation

Let’s begin.

What is a Quadratic Equation?

Before diving into the coding part of this post, let’s first understand what exactly is a quadratic equation? This section will give you a good understanding of quadratic equations which will help in understanding the algorithm. So, let’s get back to the solution. An equation of degree 2 is known as a quadratic equation. If you’re not familiar with the term ‘degree’, it is an order of an equation and its value is equal to the largest exponent present in an equation.

Standard Form

Let’s see what is the standard form of a quadratic equation, which will help you in identifying them quickly.

ax2 + bx + c = 0 is the standard form of a quadratic equation where the values of variables a, b, c is already known. The value of x is unknown and a not equal to 0.

When you plot a quadratic equation on a graph, you’ll get a curve (parabola). The points at which this equation cuts the axis are its roots. Generally, there are 2  roots of a quadratic equation. Let’s discuss the details of roots of a quadratic equation. 

Types of Roots

There are a few different ways to find the roots of a given quadratic equation. Such as, factoring the given quadratic equation, using the complete square formula and the last method involves using the quadratic formula to find the roots. I will stick to the last method as it has fewer drawbacks compared to the other methods.

Let’s consider our quadratic equation is in standard form ax2 + bx + c = 0, then the formula we can use is –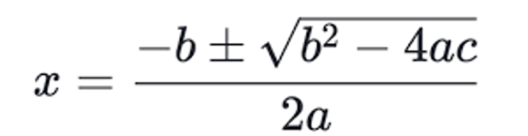 

Now, let’s talk about roots. Basically, the term inside the square-root (b2 – 4ac) in the numerator is also known as the discriminant. It can tell you more about the nature of the roots of the quadratic equation. Let’s have a look

1. If the value of the discriminant is Positive, that means we have 2 roots which are real in nature.
2. If its value is negative, you have a pair of roots which are Complex in nature (eg- 5i, 8i).
3. If it is 0, you get 2 roots having equal value and real in nature.

Now that you have a deep understanding of quadratic equations and their roots, we are good to start with the algorithm and it actually feels amazing when you’ll implement what you’ve learned in a real-world problem.

Understanding the Algorithm

Step by step let’s understand how we can write a program that can be used to find the roots of a quadratic equation.

1. 1. First, we will ask the user for the values of a, b, and c to form the quadratic equation.
   2. Once you have the values, you need to check if the value of a, entered is not 0. If it’s 0 our x2 term will be 0 and our equation won’t be quadratic anymore.
   3. Now, you have a valid quadratic equation so you can calculate its discriminant value.
   4. After getting the discriminant value, you can check for the 3 conditions discussed above to know the nature of the roots.
   5. After knowing the nature, you can calculate its roots.

Let’s now look into the C program to find the roots of a quadratic equation.

C program to find the roots of a Quadratic Equation

#include<stdio.h> 
#include<math.h> 
#include<conio.h>
#include<stdlib.h> 

/*Function to know the nature of roots and calculate the roots of given quadratic equation*/
void RootsofQuadratic(int a, int b, int c) 
{ 
    
    if (a == 0)  /*Checking for value of a*/
    { 
        printf("The value of a cannot be 0"); 
        return; 
    } 
  
    int d = b*b - 4*a*c; 
    double SquarerootDescriminant = sqrt(abs(d)); 
  
    if (d > 0) 
    { 
        printf("The Roots are Real in Nature n"); 
        printf("%fn%f",(double)(-b + SquarerootDescriminant)/(2*a) 
            , (double)(-b - SquarerootDescriminant)/(2*a)); 
    } 
    else if (d == 0) 
    { 
        printf("The roots are equal and Real in Nature n"); 
        printf("%f",-(double)b / (2*a)); 
    } 
    else // d < 0 
    { 
        printf("The Roots are Complex in Nature n"); 
        printf("%f + i%fn%f - i%f", -(double)b / (2*a),SquarerootDescriminant 
            ,-(double)b / (2*a), SquarerootDescriminant); 
    } 
}  
int main() 
{ 
    int a;
	int b;
	int c;
   printf("For a quadratic equation of form ax2 + bx + c = 0 enter values of a, b, cn");
   scanf("%d%d%d", &a, &b, &c);	 /*Asking for input*/
    RootsofQuadratic(a, b, c); 
    return 0; 
}

Output:

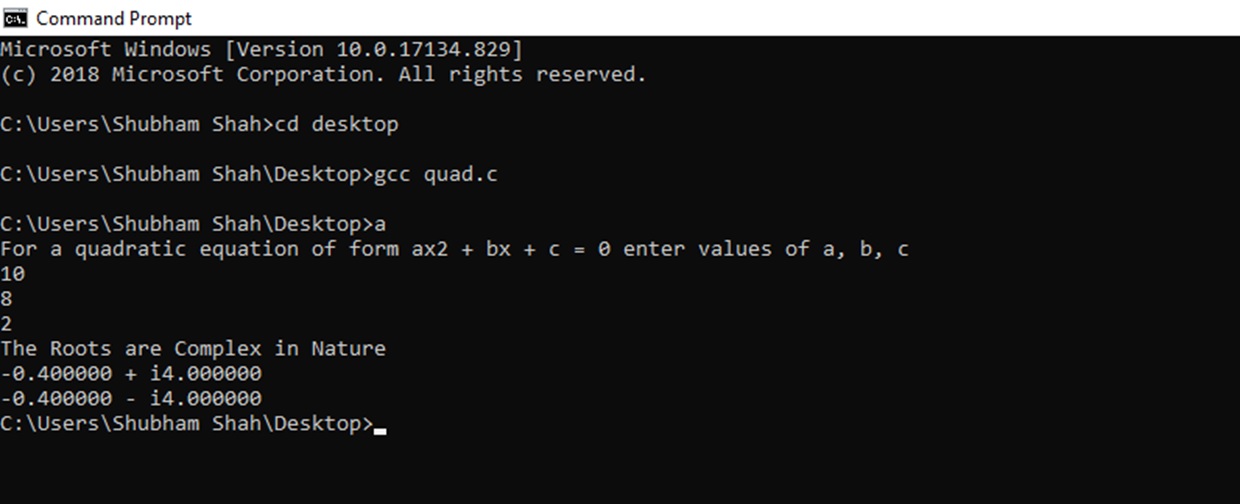
We received 2 complex roots for the values entered. Next time if you have a complex quadratic equation to solve, this program will definitely save you some time.

That’s all for this article. I hope you have understood the concept and the C program to find the roots of a quadratic equation.

If you come across any questions, feel free to ask all your questions in the comments section of “quadratic equation in C” and our team will be glad to answer.