Full Stack Web Development Internship Program
- 29k Enrolled Learners
- Weekend/Weekday
- Live Class
This article will give you a complete overview of the working of heap sort and later we will learn to implement a Binary Heap in Java.
Here is the agenda for this article:
Let’s begin!
Heap is basically a tree based data structure. It has nodes. Node comprises of certain elements. Every node contains one element.
Nodes may have children. If in case there are no children, it is called a Leaf.
There are two rules to be followed:
Heaps are extremely efficient in extracting the least or greatest element.
Let’s move on to min heap now!
Also read: Heap Sort in C
Min heap is a complete binary tree in which the value of root element is less than or equal to either of the child element.
Representation of min heap
Arr[(i-1) / 2]: this will return the parent node.
Arr[(2*i) + 1]: this will return the left child node.
Arr[(2*i) + 2]: this will return the right child node.
There are certain methods of Min Heap:
Moving on to Max heap now.
Max heap is a complete binary tree in which the value of root element is greater than or equal to either of the child element.
Max heap consists of several methods too!
Diagram:
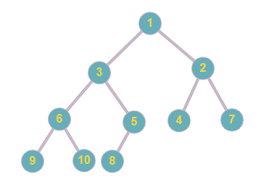
The diagram above shows the binary heap in Java. As you have learned that there are two heaps: Min heap and Max heap, here is a diagram:
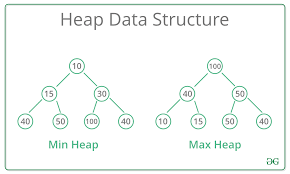
Now, moving on to our next segment, we will see how to implement a binary heap in Java.
Code:
public class BinaryHeap {
private static final int d= 2;
private int[] heap;
private int heapSize;
/**
* This will initialize our heap with default size.
*/
public BinaryHeap(int capacity){
heapSize = 0;
heap = new int[ capacity+1];
Arrays.fill(heap, -1);
}
/**
* This will check if the heap is empty or not
* Complexity: O(1)
*/
public boolean isEmpty(){
return heapSize==0;
}
/**
* This will check if the heap is full or not
* Complexity: O(1)
*/
public boolean isFull(){
return heapSize == heap.length;
}
private int parent(int i){
return (i-1)/d;
}
private int kthChild(int i,int k){
return d*i +k;
}
/**
* This will insert new element in to heap
* Complexity: O(log N)
* As worst case scenario, we need to traverse till the root
*/
public void insert(int x){
if(isFull())
throw new NoSuchElementException("Heap is full, No space to insert new element");
heap[heapSize++] = x;
heapifyUp(heapSize-1);
}
/**
* This will delete element at index x
* Complexity: O(log N)
*
*/
public int delete(int x){
if(isEmpty())
throw new NoSuchElementException("Heap is empty, No element to delete");
int key = heap[x];
heap[x] = heap[heapSize -1];
heapSize--;
heapifyDown(x);
return key;
}
/**
* This method used to maintain the heap property while inserting an element.
*
*/
private void heapifyUp(int i) {
int temp = heap[i];
while(i>0 && temp > heap[parent(i)]){
heap[i] = heap[parent(i)];
i = parent(i);
}
heap[i] = temp;
}
/**
* This method used to maintain the heap property while deleting an element.
*
*/
private void heapifyDown(int i){
int child;
int temp = heap[i];
while(kthChild(i, 1) < heapSize){
child = maxChild(i);
if(temp < heap[child]){ heap[i] = heap[child]; }else break; i = child; } heap[i] = temp; } private int maxChild(int i) { int leftChild = kthChild(i, 1); int rightChild = kthChild(i, 2); return heap[leftChild]>heap[rightChild]?leftChild:rightChild;
}
/**
* This method used to print all element of the heap
*
*/
public void printHeap()
{
System.out.print("nHeap = ");
for (int i = 0; i < heapSize; i++)
System.out.print(heap[i] +" ");
System.out.println();
}
/**
* This method returns the max element of the heap.
* complexity: O(1)
*/
public int findMax(){
if(isEmpty())
throw new NoSuchElementException("Heap is empty.");
return heap[0];
}
public static void main(String[] args){
BinaryHeap maxHeap = new BinaryHeap(10);
maxHeap.insert(10);
maxHeap.insert(4);
maxHeap.insert(9);
maxHeap.insert(1);
maxHeap.insert(7);
maxHeap.insert(5);
maxHeap.insert(3);
maxHeap.printHeap();
maxHeap.delete(5);
maxHeap.printHeap();
}
}
With this, we come to an end of this article on Binary Heap in Java. Check out the Java Online Training by Edureka, a trusted online learning company with a network of more than 250,000 satisfied learners spread across the globe. Edureka’s Java J2EE and SOA training and certification course is designed for students and professionals who want to be a Java Developer. The course is designed to give you a head start into Java programming and train you for both core and advanced Java concepts along with various Java frameworks like Hibernate & Spring.
Got a question for us? Please mention it in the comments section of this “Java ArrayList” blog and we will get back to you as soon as possible.
| Course Name | Date | Details |
|---|---|---|
| Java Course Online | Class Starts on 3rd August,2024 3rd August SAT&SUN (Weekend Batch) | View Details |
| Java Course Online | Class Starts on 28th September,2024 28th September SAT&SUN (Weekend Batch) | View Details |
 REGISTER FOR FREE WEBINAR
REGISTER FOR FREE WEBINAR  Thank you for registering Join Edureka Meetup community for 100+ Free Webinars each month JOIN MEETUP GROUP
Thank you for registering Join Edureka Meetup community for 100+ Free Webinars each month JOIN MEETUP GROUP
edureka.co
