Python Programming Certification Course
- 66k Enrolled Learners
- Weekend/Weekday
- Live Class
Bayesian Networks have given shape to complex problems that provide limited information and resources. It’s being implemented in the most advancing technologies of the era such as Artificial Intelligence and Machine Learning. Having such a system is a need in today’s technology-centric world. Keeping this in mind, this article is completely dedicated to the working of Bayesian Networks and how they can be applied to solve convoluted problems.
To get in-depth knowledge of Artificial Intelligence and Machine Learning, you can enroll for live Machine Learning Engineer Master Program by Edureka with 24/7 support and lifetime access.
Here’s a list of topics that I’ll be covering in this blog:
🐍 Ready to Unleash the Power of Python? Sign Up for Edureka’s Comprehensive Online Instructor led Python Training with access to hundreds of Python learning Modules and 24/7 technical support.
A Bayesian Network falls under the category of Probabilistic Graphical Modelling (PGM) technique that is used to compute uncertainties by using the concept of probability. Popularly known as Belief Networks, Bayesian Networks are used to model uncertainties by using Directed Acyclic Graphs (DAG).
This brings us to the question:
A Directed Acyclic Graph is used to represent a Bayesian Network and like any other statistical graph, a DAG contains a set of nodes and links, where the links denote the relationship between the nodes.
The nodes here represent random variables and the edges define the relationship between these variables. But what do these graphs model? What output can you get from a DAG?
A DAG models the uncertainty of an event occurring based on the Conditional Probability Distribution (CDP) of each random variable. A Conditional Probability Table (CPT) is used to represent the CPD of each variable in the network.
Before we move any further, let’s understand the basic math behind Bayesian Networks.
As mentioned earlier, Bayesian models are based on the simple concept of probability. So let’s understand what conditional probability and Joint probability distribution mean.
Joint Probability is a statistical measure of two or more events happening at the same time, i.e., P(A, B, C), The probability of event A, B and C occurring. It can be represented as the probability of the intersection two or more events occurring.
Conditional Probability of an event X is the probability that the event will occur given that an event Y has already occurred.
p(X| Y) is the probability of event X occurring, given that event, Y occurs.
To learn more about the concepts of statistics and probability, you can go through this, All You Need To Know About Statistics And Probability blog.
Now let’s look at an example to understand how Bayesian Networks work.
Let’s assume that we’re creating a Bayesian Network that will model the marks (m) of a student on his examination. The marks will depend on:
Exam level (e): This is a discrete variable that can take two values, (difficult, easy)
IQ of the student (i): A discrete variable that can take two values (high, low)
The marks will intern predict whether or not he/she will get admitted (a) to a university.
The IQ will also predict the aptitude score (s) of the student.
With this information, we can build a Bayesian Network that will model the performance of a student on an exam. The Bayesian Network can be represented as a DAG where each node denotes a variable that predicts the performance of the student.
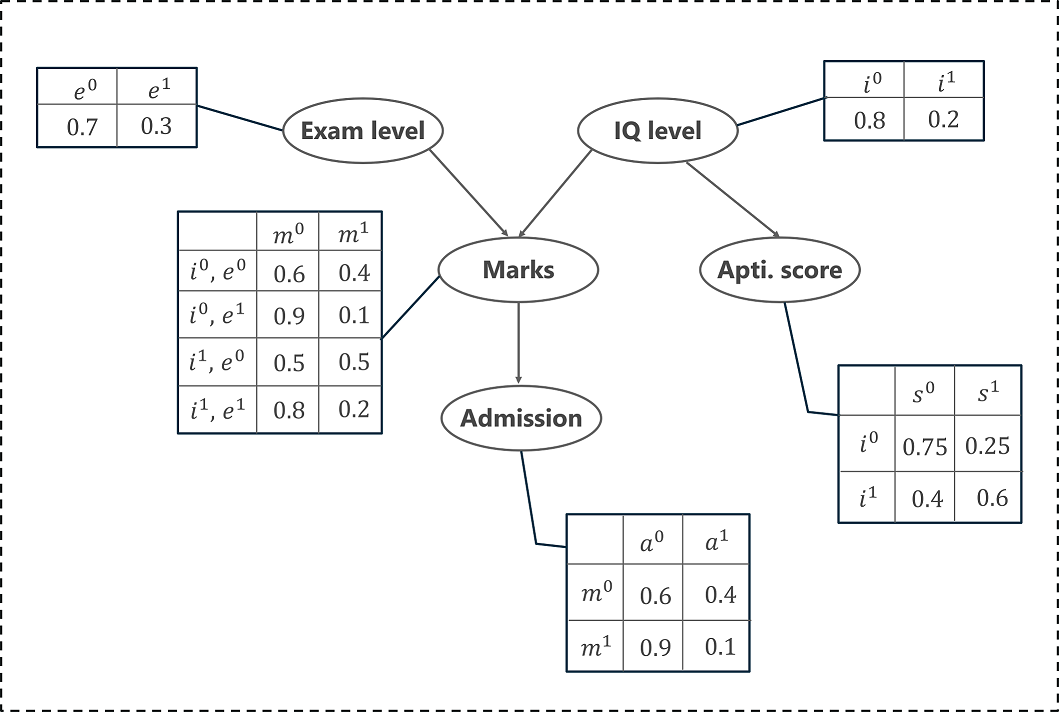
Above I’ve represented this distribution through a DAG and a Conditional Probability Table. We can now calculate the Joint Probability Distribution of these 5 variables, i.e. the product of conditional probabilities:
![]()
Here,
p(a | m) represents the conditional probability of a student getting an admission based on his marks.
p(m | I, e) represents the conditional probability of the student’s marks, given his IQ level and exam level.
p(i) denotes the probability of his IQ level (high or low)
p(e) denotes the probability of the exam level (difficult or easy)
p(s | i) denotes the conditional probability of his aptitude scores, given his IQ level
The DAG clearly shows how each variable (node) depends on its parent node, i.e., the marks of the student depends on the exam level (parent node) and IQ level (parent node). Similarly, the aptitude score depends on the IQ level (parent node) and finally, his admission into a university depends on his marks (parent node). This relationship is represented by the edges of the DAG.
If you notice carefully, we can see a pattern here. The probability of a random variable depends on his parents. Therefore, we can formulate Bayesian Networks as:
![]()
Where, X_i denotes a random variable, whose probability depends on the probability of the parent nodes, 𝑃𝑎𝑟𝑒𝑛𝑡𝑠(𝑋_𝑖).
Simple, isn’t it?
Bayesian Networks are one of the simplest, yet effective techniques that are applied in Predictive modeling, descriptive analysis and so on.
To make things more clear let’s build a Bayesian Network from scratch by using Python.
In this demo, we’ll be using Bayesian Networks to solve the famous Monty Hall Problem. For those of you who don’t know what the Monty Hall problem is, let me explain:
The Monty Hall problem named after the host of the TV series, ‘Let’s Make A Deal’, is a paradoxical probability puzzle that has been confusing people for over a decade.
So this is how it works. The game involves three doors, given that behind one of these doors is a car and the remaining two have goats behind them. So you start by picking a random door, say #2. On the other hand, the host knows where the car is hidden and he opens another door, say #1 (behind which there is a goat). Here’s the catch, you’re now given a choice, the host will ask you if you want to pick door #3 instead of your first choice i.e. #2.

Is it better if you switch your choice or should you stick to your first choice?
This is exactly what we’re going to model. We’ll be creating a Bayesian Network to understand the probability of winning if the participant decides to switch his choice.
A short disclaimer before we get started with the demo.
I’ll be using Python to implement Bayesian Networks and if you don’t know Python, you can go through the following blogs:
Now let’s get started.
The first step is to build a Directed Acyclic Graph.
The graph has three nodes, each representing the door chosen by:
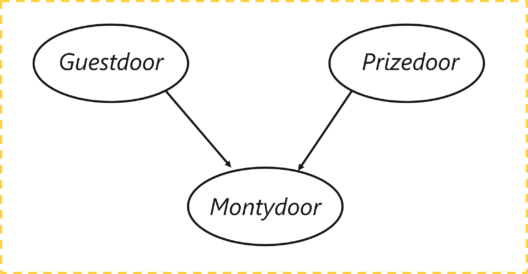
Let’s understand the dependencies here, the door selected by the guest and the door containing the car are completely random processes. However, the door Monty chooses to open is dependent on both the doors; the door selected by the guest, and the door the prize is behind. Monty has to choose in such a way that the door does not contain the prize and it cannot be the one chosen by the guest.
#Import required packages
import math
from pomegranate import *
# Initially the door selected by the guest is completely random
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# The door containing the prize is also a random process
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# The door Monty picks, depends on the choice of the guest and the prize door
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
#Building the Bayesian Network
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()
In the above code ‘A’, ‘B’, ‘C’, represent the doors picked by the guest, prize door and the door picked by Monty respectively. Here we’ve drawn out the conditional probability for each of the nodes. Since the prize door and the guest door are picked randomly there isn’t much to consider. However, the door picked by Monty depends on the other two doors, therefore in the above code, I’ve drawn out the conditional probability considering all possible scenarios.
The next step is to make predictions using this model. One of the strengths of Bayesian networks is their ability to infer the values of arbitrary ‘hidden variables’ given the values from ‘observed variables.’ These hidden and observed variables do not need to be specified beforehand, and the more variables which are observed the better the inference will be on the hidden variables.
Now that we’ve built the model, it’s time to make predictions.
beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}
In the above code snippet, we’ve assumed that the guest picks door ‘A’. Given this information, the probability of the prize door being ‘A’, ‘B’, ‘C’ is equal (1/3) since it is a random process. However, the probability of Monty picking ‘A’ is obviously zero since the guest picked door ‘A’. And the other two doors have a 50% chance of being picked by Monty since we don’t know which is the prize door.
beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B
In the above code snippet, we’ve provided two inputs to our Bayesian Network, this is where things get interesting. We’ve mentioned the following:
Notice the output, the probability of the car being behind door ‘C’ is approx. 66%. This proves that if the guest switches his choice, he has a higher probability of winning. Though this might seem confusing to some of you, it’s a known fact that:
Bayesian Networks are used in such cases that involve predicting uncertain tasks and outcomes. In the below section you’ll understand how Bayesian Networks can be used to solve more such problems.
Bayesian Networks have innumerable applications in a varied range of fields including healthcare, medicine, bioinformatics, information retrieval and so on. Here’s a list of real-world applications of the Bayesian Network:
Disease Diagnosis: Bayesian Networks are commonly used in the field of medicine for the detection and prevention of diseases. They can be used to model the possible symptoms and predict whether or not a person is diseased.
Optimized Web Search: Bayesian Networks are used to improve search accuracy by understanding the intent of a search and providing the most relevant search results. They can effectively map users intent to the relevant content and deliver the search results.
Spam Filtering: Bayesian models have been used in the Gmail spam filtering algorithm for years now. They can effectively classify documents by understanding the contextual meaning of a mail. They are also used in other document classification applications.
Gene Regulatory Networks: GRNs are a network of genes that are comprised of many DNA segments. They are effectively used to communicate with other segments of a cell either directly or indirectly. Mathematical models such as Bayesian Networks are used to model such cell behavior in order to form predictions.
Biomonitoring: Bayesian Networks play an important role in monitoring the quantity of chemical dozes used in pharmaceutical drugs.
Now that you know how Bayesian Networks work, I’m sure you’re curious to learn more. Here’s a list of blogs that will help you get started with other statistical concepts:
With this, we come to the end of this blog. If you have any queries regarding this topic, please leave a comment below and we’ll get back to you.
Stay tuned for more blogs on the trending technologies.
If you wish to enroll for a complete course on Artificial Intelligence and Machine Learning, Edureka has a specially curated Machine Learning Engineer Master Program that will make you proficient in techniques like Supervised Learning, Unsupervised Learning, and Natural Language Processing. It includes training on the latest advancements and technical approaches in Artificial Intelligence & Machine Learning such as Deep Learning, Graphical Models and Reinforcement Learning.
 Thank you for registering Join Edureka Meetup community for 100+ Free Webinars each month JOIN MEETUP GROUP
Thank you for registering Join Edureka Meetup community for 100+ Free Webinars each month JOIN MEETUP GROUPedureka.co