What is Alpha Beta Pruning in Artificial Intelligence?

The word pruning really reminds of cutting down branches, or to those familiar with data science, it reminds of post and pre-pruning in trees. Alpha-beta pruning is essentially pruning of useless branches. We’ll be discussing the following pointers:

• MinMax Algorithm
• Alpha-Beta Pruning

In this blog, we’ll be going over alpha-beta pruning and how we can use it to create strategies in games with multiple paths. Each one of these paths leads to a different outcome. When we have such an enormous amount of moves, (eg in chess or sudoku) we really need to strategize the game in a well-defined manner. Such games end up evolving and make a weirdly high number of possible outcomes. So we need to think of how we can choose the best possible move. This has to be achieved without spending the amount of time it took for cats to populate the Earth.

Minmax Algorithm

The minimax algorithm is more intuitive to understand in terms of a brute-force approach. It tries to see every possible outcome and then tries to optimize whatever options it has in hand.

Just like Sudoku, we can essentially end up generating a tree consisting of branches going to a depth containing all the set of all possible moves made by the player(s) in the game. We will next, need to traverse this tree.

The downward triangle represents a location in the tree where minimax will minimize the opponent’s advantage. Whereas, the upward triangles are the locations where minimax maximizes the user’s advantage.

Intuitively, to know a player’s advantage, it first needs to know which path leads to victory. This is where the brute force approach comes into the picture. This essentially means that the algorithm has to traverse to the bottom of the tree and go through every possible move. Next, it has to assign some weight (e.g., +1 for a win and -1 for a loss), and propagate this weight up through the tree.

Alpha-Beta Pruning

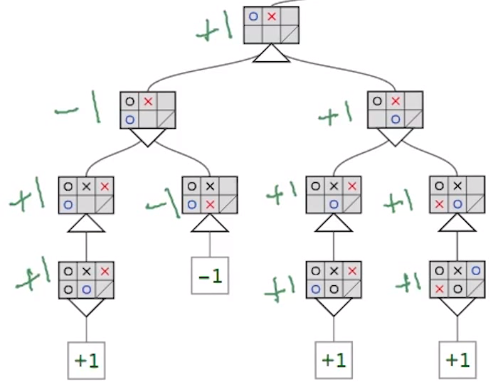
Alpha Beta Pruning is all about reducing the size (pruning) of our search tree. While a brute-force approach is an easier approach to use, it doesn’t necessarily mean it is the most optimal approach. Many times, one doesn’t need to visit all possible branches to come up with the best possible solution in hand.

Thus we need to provide the min-max algorithm with some stopping criteria using which it would stop searching a region of the tree once it finds the guaranteed minimum or maximum at that level. This would prevent the algorithm from using additional computational time, making it much more responsive and fast.

The original min-max algorithm performs traversals of the tree in a left to right fashion while also going to the deepest possible depth of the tree. This essentially is a depth-first approach. It then discovers values that must be assigned to nodes directly above it, without ever looking at other branches of the tree.

Thus, the addition of the stopping condition makes min-max take decisions like it used to previously but it optimizes the performance aspect of the algorithm.

In the image below, we have a tree with various scores assigned to each node. Some nodes are shaded in red, indicating there’s no need to review them.

At the bottom left of the tree, minimax goes through the values 5 and 6 on the bottom max level. It determines that 5 must be assigned to the min level right above it.

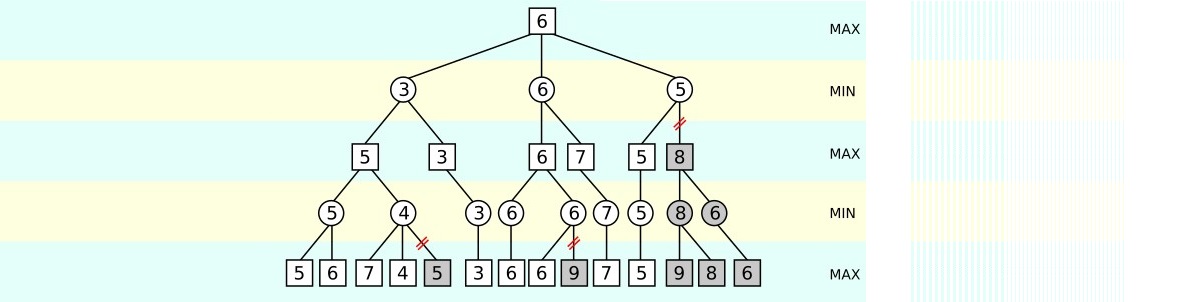
But, after looking at 7 and 4 of the right max level branch, it realizes that the above min level node must be assigned a maximum value of 4. Since the second max level right above the first min level will take the maximum between 5 and at most 4, it’s clear that it’ll choose 5. Following this, it would continue traversing the tree to perform the same exact set of operations within the tree’s other branches.

Concluding, we can easily understand how alpha-beta pruning acts as a great optimization over the min-max algorithm and how these algorithms are the foundation of state-space searching techniques, paving the way for much more advanced approaches to solving such problems.

With this, we come to an end of this Alpha Beta Pruning in Artificial Intelligence article.

So, this article is based on the AI and Deep Learning with TensorFlow Course is curated by industry professionals as per the industry requirements & demands. You will master the concepts such as SoftMax function, Autoencoder Neural Networks, Restricted Boltzmann Machine (RBM) and work with libraries like Keras & TFLearn. The course has been specially curated by industry experts with real-time case studies. 

Got a question for us? Please mention it in the comments section of “Alpha Beta Pruning in Artificial Intelligence” and we will get back to you.